Arithmetique spé maths

[Prapaline]

Bonjour,
pour la fin des vacances, j'ai un exercice à faire en spé maths sur lequel je ne vois pas comment il faut le résoudre, pouvez vous m'aider, l'énoncé est le suivant : Démontrer que pour deux couples d'entiers (a,b) et (c,d) distincts, les nombres
a√2 + b√3 et c√2 + d√3 sont distincts.

Je vous remercie de l'aide.

[hdci]

Bonjour,

As-tu déjà essayé quelque chose ?
En général, une idée classique pour montrer que "quelque chose est faux" (ici "deux nombres ne sont pas égaux") est de raisonner par l'absurde

[Prapaline]

J'ai essayer un raisonnement par l'absurde mais il m'amène à une équation que je ne peux pas résoudre, ensuite j'ai essayer une réciproque mais c'est pareil je ne sais pas résoudre une équation à quatre inconnu. Mais la professeur nous a conseillé d'utiliser la réciproque. Si vous avez des idées, de comment faire je ne vois vraiment pas.

[hdci]

Par l'absurde, on suppose que 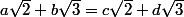ce qui donne


ou encore que est rationnel (puisque et )

Après, un entier au carré est pair ssi l'entier est pair, et un entier au carré est multiple de 3 ssi l'entier est multiple de 3, et en écrivant racine de deux tiers sous forme de fraction irréductible, on arrive à la contradiction que cette fraction se simplifie par 6 donc n'est pas irréductible

[aymanemaysae]

Bonjour ;


Les couples des nombres entiers relatifs et sont distincts ;

donc on a : ou .

Par l'absurde , on va supposer qu'on a : .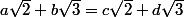

Je crois qu'il ne te reste qu'une seule ligne pour conclure .

[Prapaline]

Je vous remercie de vos réponse, je viens de comprendre comment il fallait faire grace à vous.

[aymanemaysae]

De rien . Bon courage .