Inéquation

[Falone]

Bonjour à tous
Je dois résoudre cette inéquation.
x^2+(10-x)(8-x)>ou= 80-x^2+(10-x)(8-x)
Voilà j'espère que vous pourrai m'aider je sais que normalement je dois utiliser delta mais je sais pas comment m'y prendre merci.

PS: c'est du niveau 1ereS

[fatal_error]

slt,

tu mets tout de la forme
ax^2+bx+c >= 0
tu factorises jor
c(x - x_1)(x - x_2) >= 0
avec x_1 et x_2 le racines de ton trinome, puis après tableau de signe

[Falone]

slt,

tu mets tout de la forme
ax^2+bx+c >= 0
tu factorises jor
c(x - x_1)(x - x_2) >= 0
avec x_1 et x_2 le racines de ton trinome, puis après tableau de signe

mais comment je met tout en forme développé puisque le premier x est au carré comment je le multiplie par un autre x? ca me fait x au cube? mais ducoup ça ferai une inéquation de degré 3 non?

[aymanemaysae]

Bonsoir;

On peut simplifier avant et le tour est joué :

x^2+(10-x)(8-x)>ou= 80-x^2+(10-x)(8-x)

[Falone]

Bonsoir;

On peut simplifier avant et le tour est joué :

x^2+(10-x)(8-x)>ou= 80-x^2+(10-x)(8-x)

C'est à dire x^2 >ou= 80-x ???

[aymanemaysae]

Non ; en simplifiant tu auras : x^2 > ou = 80 - x^2 ; sauf si ton énoncé est erroné .

[Falone]

Non ; en simplifiant tu auras : x^2 > ou = 80 - x^2 ; sauf si ton énoncé est erroné .

Je comprend pas comment simplifier c'est ça le problème

[aymanemaysae]

Tu as initialement :
x^2+(10-x)(8-x)>ou= 80-x^2+(10-x)(8-x) ;
donc tu peux simplifier par (10-x)(8-x) qui se trouve dans les deux
parties de l'inéquation , pour obtenir : x^2 > ou = 80 - x^2 .

Tu as maintenant x^2 dans la partie gauche de l'inéquation et - x^2 dans la partie droite de l'inéquation ;
donc - x^2 peut passer dans la partie gauche de l'inéquation mais en changeant de signe ,
donc on a : x^2 + x^2 > ou = 80 ;
donc : 2 x^2 > ou = 80 .

Peux-tu continuer maintenant ?

[Falone]

Tu as initialement :
x^2+(10-x)(8-x)>ou= 80-x^2+(10-x)(8-x) ;
donc tu peux simplifier par (10-x)(8-x) qui se trouve dans les deux
parties de l'inéquation , pour obtenir : x^2 > ou = 80 - x^2 .

Tu as maintenant x^2 dans la partie gauche de l'inéquation et - x^2 dans la partie droite de l'inéquation ;
donc - x^2 peut passer dans la partie gauche de l'inéquation mais en changeant de signe ,
donc on a : x^2 + x^2 > ou = 80 ;
donc : 2 x^2 > ou = 80 .

Peux-tu continuer maintenant ?

Oui merc, j'ai trouvé 2x^2-1-x+240
c'est ça?

[Falone]

2x^2-16x+240 pardon

[aymanemaysae]

Non , je ne crois pas que c'est juste , car on a : 2x^2 > ou = 80 ;
donc en divisant les deux parties par 2 , on obtient : x^2 > ou = 40 .

Tu dois maintenant remarquer que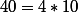 ; donc 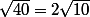et utiliser
une identité remarquable : a² - b² = (a - b)(a + b) .

Ps : l'énoncé initial de l'exercice est-il vraiment l'énoncé donné par ton prof ?