Je cherche à montrer le résultat suivant :
Soit
Alors,
J'ai essayé de développer
Quelqu'un aurait-il une solution ?
Merci d'avance !
Preuve d'une inégalité sur les sommes
2 messages
- Page 1 sur 1
Preuve d'une inégalité sur les sommes
par wartenberg » 12 Sep 2019, 17:23
Bonjour,
Je cherche à montrer le résultat suivant :
Soit
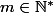
et  \: \in \: \mathbb{R}^m)
.
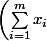Alors,^2 \leq m \times \sum_{i=1}^{m}{x_i^2})
.
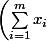J'ai essayé de développer^2 = \sum_{i=1}^{m}{x_i^2} + 2 \sum_{j<k}{x_j x_k)
, puis d'écrire que , \; \forall \: k,j \:)
mais ça ne me donne pas grand chose...
Quelqu'un aurait-il une solution ?
Merci d'avance !
Je cherche à montrer le résultat suivant :
Soit
Alors,
J'ai essayé de développer
Quelqu'un aurait-il une solution ?
Merci d'avance !
Re: Preuve d'une inégalité sur les sommes
par infernaleur » 12 Sep 2019, 18:17
Salut,
Si tu connais l’inégalité de Cauchy-Schwarz c’est direct.
Si tu connais l’inégalité de Cauchy-Schwarz c’est direct.
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :