Application linéaire et polynôme

[Tequinox]

Bonjour, je n'arrive pas à faire l'exercice suivant :

Soit f l’application linéaire : P (X) ==> P' (X)

Quelle est la matrice de f dans la base 1,X, (X^2)/2 , (x^3)/6 , (x^4)/24

Je dois retrouver la bonne proposition d'un qcm parmi 4 matrices, sauf que la matrice que je trouve est différente des 4 réponses, je dois me tromper de méthode mais je ne trouve pas comment réaliser autrement :

Pour chaque colonne je remplace le X par l’élément de la base :
P(1) = 0
P(X)= 1
P(X²/2)= 2X
P(x^3)/6 =X²/2
P(x^4)/24=(x^3)/6

et j'obtient la matrice :
0 1 0 0 0
0 0 2 0 0
0 0 0 1/2 0
0 0 0 0 1/6
0 0 0 0 0

Pouvez-vous m'aider, merci.

[aviateur]

Bonjour
C'est pas ça, il n'y a que des 1 comme par exemple c'est 1/6 mais 1.
En effet si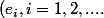 c'est la base, tu as exactement

[pascal16]

1,X, (X^2)/2 , (x^3)/6 , (x^4)/24

1-> 0 soit " 0 ..." : ok
X-> 1 soit " 1 0 ..." : ok

X²/2 -> X soit "0 1..." dans la base 1,X, ...

(x^3)/6 -> X²/2 soit "0 0 1..." dans la base 1,X, (X^2)/2 ,..

[Tequinox]

D'accord merci, j'ai compris pour ce genre de polynôme.

J'ai un autre problème, sur une autre question :

Soit f l’application linéaire : P (X) ==> P (0) + P(1)*X + P(2)*X²

Dans la base : 1, X - 1 , ( X - 1 )²

Je ne comprend pas par quoi remplacer les P(0) P(1) et P(2).

Merci,

[Tequinox]

Si quelqu'un pourrais m'aider, je n'y arrive toujours pas , merci

[mathelot]

Soit f l’application linéaire : P (X) ==> P (0) + P(1)*X + P(2)*X²

Dans la base : 1, X - 1 , ( X - 1 )²

à traduire dans la base



la 1ère colonne de la matrice de f est donc:

[Tequinox]

Bonjour, merci de votre réponse mais je ne comprend pas comment vous trouvez la deuxièmes lignes de f(1)

[mathelot]

j'exprime f(1) dans la base



Par identification, ça me donne un système d'inconnues alpha,béta,gamma

[Tequinox]

Je suis perdu je ne vois pas du tout ce qu'il faut faire.

[Tequinox]

J'ai essayer de trouver un système à partir de l'équitation, mais je n'y arrive pas, si quelqu’un peut m'aider, merci

[pascal16]

sauf erreur de calcul :

1+x+x² = a*1+b*(x-1)+c*(x-1)²
= a + bx -b + cx² -2cx -c
= (a-b-c) + (b-2c)x + c x²

par identification de polynômes :
d'où c
d'où b
d'où a

[Tequinox]

J'avais effectivement trouvé la même équation, mais je ne vois pas comment en déduire le résultat donné plus haut.

[pascal16]

on identifie
1.x² = c.x²

que vaut c ?

[Tequinox]

Merci je viens de comprendre comment trouver la première ligne, en remplaçant je trouve c=1 qui me permet de trouver b=3 et a=3

Pour la deuxième colonne, j'ai essayé de faire la même chose mais avec f(X-1)=1+(X-1)+(X-1)² .

Mais je n'arrive pas à l'exprimer dans la base 1, (X-1), (X-1)²

[pascal16]

si j'ai pas raté une ligne :
P(X)=X-1
P(0) = -1
P(1) = 0
P(2)= 1
f(X-1) = -1*1 + 0*X + 1*X² =-1 + X²

[Tequinox]

Si je continu : -1 + X² = -a*1 + c*(x-1)²
= -a + c*x² + c - 2cx
=(c-a) -2c*x + c*x² = -1 + X²

donc c=1 et a=2 ?

[pascal16]

donc c=1 et a=2 ? NON

-1 + X² = (a-b-c) + (b-2c)x + c x²

c=1
b-2c=0
...