Je ne vois pas comment partir pour trouver la loi de Y
Convergence en loi
7 messages
- Page 1 sur 1
Convergence en loi
par JohnnySuave » 24 Jan 2019, 15:58
Soit )
(où P est la loi de Poisson) et Y telle que :
=1\\)
et la loi conditionnelle de Y sachant [X=n] est la loi binomiale B(n,p).
Je ne vois pas comment partir pour trouver la loi de Y
Je ne vois pas comment partir pour trouver la loi de Y
Re: Convergence en loi
par LB2 » 24 Jan 2019, 21:35
Bonjour,
il faut utiliser que tu connais la loi conditionnelle de Y sachant [X=n]
Les évènements [X=n] forment un système complet d'évènement (SCE) et tu connais la loi de X, donc ...
il faut utiliser que tu connais la loi conditionnelle de Y sachant [X=n]
Les évènements [X=n] forment un système complet d'évènement (SCE) et tu connais la loi de X, donc ...
Re: Convergence en loi
par JohnnySuave » 24 Jan 2019, 21:56
Je ne sais pas si je traduit correctement l'énoncé en fait
Est-ce que c'est juste :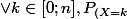}(Y=k)=\begin{pmatrix}<br />n\\k <br /><br />\end{pmatrix}<br />p^{k}(1-p)^{n-k})
Est-ce que c'est juste :
Re: Convergence en loi
par LB2 » 24 Jan 2019, 22:43
pas tout à fait, tu conditionnes par l'évènement (X=n) et pas (X=k), sinon ça ne veut rien dire...
Re: Convergence en loi
par Ben314 » 24 Jan 2019, 23:12
Salut,
Tes hypothèses, c'est ça :
\ \forall k\!\in\!\N,\ P(Y\!=\!k)\!=\!e^{-\lambda}\frac{\lambda^k}{k!})
\ \forall n\!\in\!\N,\ \forall k\!\in\!\N,\ \dfrac{P(Y\!=\!k\text{ et }X\!=\!n)}{P(X\!=\!n)}\!=\!{n\choose k}p^kq^{n-k}\ \ (=0\text{ si }k\!>\!n})\ \text{ avec }\ q\!=\!1\!-\!p)
<br />=\sum_{n\geq 0}\!\!P(Y\!=\!k\text{ et }X\!=\!n)<br />=P(Y\!=\!k)<br />=e^{-\lambda} \frac{\lambda^k}{k!})
<br />=e^{-\lambda}\frac{\mu^k}{k!}\ \text{ avec }\ \mu\!=\!\frac{q}{p}\lambda)
^{k-\ell}{k\choose \ell}\!\sum_{n\geq k}\!\!{n\choose k}q^nP(X\!=\!n)\!\bigg)<br />=e^{-\lambda}\sum_{k\geq\ell}(-1)^{k-\ell}{k\choose \ell}\frac{\mu^k}{k!}<br />=e^{-\lambda}\frac{\mu^\ell}{\ell!}\!\!\sum_{m\geq0}\!\!\frac{(-\mu)^m}{m!})
\!\sum_{k=\ell}^n\!(-1)^{k-\ell}{k\choose \ell}{n\choose k}\!\bigg)<br />=\frac{\mu^\ell}{\ell!}e^{-(\lambda+\mu)}<br />=\frac{\mu^\ell}{\ell!}e^{-\frac{\lambda}{p}})
^{k-\ell}{k\choose \ell}{n\choose k}<br />={n\choose\ell}\sum_{k=\ell}^n\!(-1)^{k-\ell}{n-\ell\choose k-\ell}<br />=\left\{\begin{matrix}1\text{ si }n\!=\!\ell\cr0\text{ si }n\!>\!\ell\end{matrix}\right.)
<br />=\frac{\mu^\ell}{\ell!}e^{-\frac{\lambda}{p}}\ <br />\text{ c'est \`a dire }\ P(X\!=\!\ell)<br />=\frac{1}{\ell!}\big(\frac{\lambda}{p}\big)^{\!\ell} e^{-\frac{\lambda}{p}})
Ce qui signifie que)
Et la loi conjointe est donnée par :
}<br />=e^{-\frac{\lambda}{p}} \dfrac{\ \ p^k\,(1\!-\!p)^{n-k}}{k!\,(n\!-\!k)!\ \ }\bigg(\dfrac{\lambda}{p}\bigg)^{\!\!n} <br />\ (=0\text{ si }k\!>\!n}))
Tes hypothèses, c'est ça :
Ce qui signifie que
Et la loi conjointe est donnée par :
Modifié en dernier par Ben314 le 25 Jan 2019, 23:11, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Convergence en loi
par LB2 » 25 Jan 2019, 01:26
Ben, je crois que tu as inversé X et Y au début: c'est X qui suit la loi de Poisson de paramètre lambda.
Du coup tu as résolu un problème intéressant (via une formule d'inversion) : si Y suit Poisson (lambda) et que Y sachant (X=n) est une Binomiale de paramètre (n,p), alors X est également une Posson, de paramètre lambda/p
Avec le "vrai" énoncé, on devrait trouver que Y suit une Poisson de paramètre (lambda*p), mais surtout le calcul est beaucoup plus simple (pas d'inversion à faire dans la somme)
J'imagine que ce résultat s'interprète très bien en terme de processus de Poisson sous-jacent (ce n'est pas encore très clair pour moi)
Du coup tu as résolu un problème intéressant (via une formule d'inversion) : si Y suit Poisson (lambda) et que Y sachant (X=n) est une Binomiale de paramètre (n,p), alors X est également une Posson, de paramètre lambda/p
Avec le "vrai" énoncé, on devrait trouver que Y suit une Poisson de paramètre (lambda*p), mais surtout le calcul est beaucoup plus simple (pas d'inversion à faire dans la somme)
J'imagine que ce résultat s'interprète très bien en terme de processus de Poisson sous-jacent (ce n'est pas encore très clair pour moi)
Re: Convergence en loi
par Ben314 » 25 Jan 2019, 09:31
Ah, tient... faudrait que j’apprenne à lire....
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :