Derniers chiffres de 3^3^3^3

[xinxin]

1)Trouver les trois derniers chiffres de 3^(3^3^3)
2) Montrer que si Xn=3^(3^...3) avec n fois 3 entre parenthèses , si n >=10, alors les Xn ont les mêmes dix derniers chiffres.
Je pense qu’il faut utiliser le théorème d’Euler fermat. Phi(10^10)=4*10^9, alors il faut connaître Xn modulo (4*10^9) pour connaître Xn+1 mod 10^10.
Pour 1), je cherche 3^3^3=3^27 mod 400, et je sais que 3^27=3^7mod 25=12 mod 25, 3^27=11 mod 16.
J’ai besoin d’un peu d’aide pour la suite

[WillyCagnes]

Bsr
3¹=3
3²=9
3³=27
3⁴=81
3⁵=243
3⁶=729
3⁷=2187
3⁸=6561
On voit que le chiffre des unités suit une séquence répétitive : 3 / 9 / 7 / 1
Donc toutes les 4 puissances on retombe sur le même chiffre des unités

[pascal16]

je cherche 3^(3^3)=3^27 mod 400
3^27=3^9*3^9*3^9 mod 400
=83*83*83 mod 400 car 3^9-49*400=83
= 187 mod 400 car 83*83*83-400*1429=187

[Ben314]

Salut,
A mon avis, si tu n'utilise que l'indicatrice d'Euler "direct", ça risque de ne pas suffire.
En fait, avoir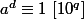 ça équivaut à avoir .
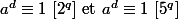Or, si est premier avec , la première congruence est vraie pour tout multiple de et la deuxième est vraie pour tout multiple de donc les deux sont vérifiées pour 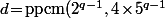qui est plus petit que ton .
En particulier, pour
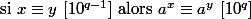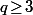ce qui prouve que, (pour et premier avec 10)

[xinxin]

Merci beaucoup ! La réponse de Ben314 est très complète ! Je calcule maintenant en utilisant la proposition de Ben: Comme 3^3^3=87[10²], 3⁸⁷ [10³]=(3²⁰)⁴*3⁷
3^20=401[10³] et 401²=801 [10³], donc (3^20)⁴=801² [10³]=601 [10³] et enfin 3⁷=2187=187 [10³],
601*187=387 [10³]
Donc 3^(3^3^3)=387 [10³]

Vous voulez bien vérifier ce que j'ai fait ?