Pour moi, ce type d'exercice, c'est plus ou moins le B-A-BA de l'utilisation des définitions des limites
(1).
Et comme c'est du "pour débutant", j'aurais tendance à présenter une preuve extrêmement détaillée pour que tout soit bien clair. Pour la question 2., ça donnerais :
On veut montrer que la limite lorsque

de
\!=\!\int_{A}^{cA}\dfrac{f(x)\!-\!\ell}{x}\,dx)
est nulle, c'est à dire que :
\!-\!0|\!<\!\varepsilon)
.
On choisi donc un
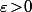
.
Par hypothèse, on a
\!=\!\ell)
, donc il existe

tel que, pour

, on ait
\!-\!\ell|\!<\!{\red ???}) ou pour le moment, on ne sait pas trop ce qu'on va mettre à la place du
ou pour le moment, on ne sait pas trop ce qu'on va mettre à la place du  mais on sait qu'on peut mettre n'importe quoi de >0 dépendant de
mais on sait qu'on peut mettre n'importe quoi de >0 dépendant de  ou tout autre chose défini précédement, mais pas de
ou tout autre chose défini précédement, mais pas de  par exemple
par exempleSi

et

sont tout les deux plus grand que

, c'est à dire si
)
alors tout les

entre

et

sont

donc ils vérifient tous
\!-\!\ell|\!<\!{\red ???})
et on a
|=\left|\int_{A}^{cA}\dfrac{f(x)\!-\!\ell}{x}\,dx\right|\mathop{\leq}\limits_{(2)}<br />\left|\int_{A}^{cA}\dfrac{{\red ???}}{x}\,dx\right|<br />={\red ???}\left|\Big[\ln(x)\Big]_{A}^{cA}\right|<br />={\red ???}\left|\ln(cA)\!-\!\ln(A)\right|<br />={\red ???}\left|\ln(c)\right|=\varepsilon)
A condition d'avoir pris plus haut
|})
en considérant "à part" le cas où
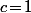
qui de toute façon est sans intérêt vu que dans ce cas là on a
\!=\!0)
pour tout

.
On a donc montré qu'il existait un

, à savoir
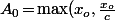)
, tel que, pour tout

, on ait
\!-\!0|\!<\!\varepsilon)
. Et comme le
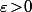
choisi au départ est quelconque, on a bien démontré le résultat voulu.
(1) Dans le sens que c'est le type d'exercice le plus simple possible où on montre quelque chose de "pas totalement évident" (intuitivement parlant) à l'aide de la définition des limites.
(2) Attention, si

, on a
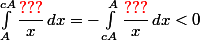
donc il faut garder une valeur absolue à droite de l'inégalité. Une façon peut-être plus prudente de rédiger est de distinguer deux cas selon que

ou pas vu que l'implication
\,dx\leq\int_\alpha^\beta g(x)\,dx)
n'est valable que si

mais que l'inégalité est "dans l'autre sens" si l'intégrale est écrite "à l'envers" c'est à dire avec

.
et que la fonction dans l'intégrale est égal à
avec
, alors
donc l’intégrale de la question 2 est bien égale à 0 (
=0 ) ?