Limite trigonometrique
6 messages
- Page 1 sur 1
limite trigonometrique
par nabil » 04 Oct 2018, 19:22
lim sin(π*sqrt(cos(x)))/x quand x tend vers 0 . s il vous plait
Re: limite trigonometrique
par pascal16 » 04 Oct 2018, 19:32
niveau lycée, sans développement limité ?
lim sin(π*sqrt(cos(x)))/x quand x tend vers 0 . s il vous plait
soit f(x) = sin(π*sqrt(cos(x)))
on reconnait lim (f(x)-f(0))/(x-0) = f'(0) si la limite existe.
f' étant assez dure à calculer
lim sin(π*sqrt(cos(x)))/x quand x tend vers 0 . s il vous plait
soit f(x) = sin(π*sqrt(cos(x)))
on reconnait lim (f(x)-f(0))/(x-0) = f'(0) si la limite existe.
f' étant assez dure à calculer
Re: limite trigonometrique
par Ben314 » 04 Oct 2018, 19:51
Salut,
Avec un peu d'effort, on y arrive par simple composition de limites classiques :
}\Big)}{x}<br />=\dfrac{\sin\Big(\pi-\pi\sqrt{\cos(x)}\Big)}{x}<br />=\dfrac{\sin\Big(\pi\big(1-\sqrt{\cos(x)}\big)\Big)}{\pi\big(1-\sqrt{\cos(x)}\big)}\!\times\!\dfrac{1-\sqrt{\cos(x)}}{x}\!\times\!\pi=\cdots)
où le premier facteur tend vers 1 car de la forme}{t})
avec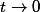 
.
Ensuite, on multiplie le numérateur et le dénominateur du deuxième facteur par le conjugué du numérateur pour virer la racine et ça doit être fini.
Avec un peu d'effort, on y arrive par simple composition de limites classiques :
où le premier facteur tend vers 1 car de la forme
Ensuite, on multiplie le numérateur et le dénominateur du deuxième facteur par le conjugué du numérateur pour virer la racine et ça doit être fini.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: limite trigonometrique
par LB2 » 04 Oct 2018, 20:21
Sinon tu peux utiliser la règle de l'Hôpital mais c'est borderline hors programme au lycée...
Re: limite trigonometrique
par pascal16 » 04 Oct 2018, 20:24
bien vu
reste le terme (1-cos(x))/x
qui est encore une forme (f(0)-f(x))/(x-0)
reste le terme (1-cos(x))/x
qui est encore une forme (f(0)-f(x))/(x-0)
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :