Stevenson123 a écrit:Exact.
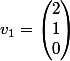
,
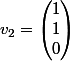
,
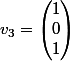
Donc pour la question (1) ça serait plutôt :
 = A\begin{pmatrix}2\\1\\0\end{pmatrix} = \begin{pmatrix}-2 & 4 & 3 \\-1 & 2 & 2\\ 0 & 0 & 0\end{pmatrix} * \begin{pmatrix}2\\1\\0\end{pmatrix} = \begin{pmatrix}0\\0\\0\end{pmatrix})
 = A\begin{pmatrix}1\\1\\0\end{pmatrix} = \begin{pmatrix}-2 & 4 & 3 \\-1 & 2 & 2\\ 0 & 0 & 0\end{pmatrix} * \begin{pmatrix}1\\1\\0\end{pmatrix} = \begin{pmatrix}2\\1\\0\end{pmatrix})
 = A\begin{pmatrix}1\\0\\1\end{pmatrix} = \begin{pmatrix}-2 & 4 & 3 \\-1 & 2 & 2\\ 0 & 0 & 0\end{pmatrix} * \begin{pmatrix}1\\0\\1\end{pmatrix} = \begin{pmatrix}1\\1\\0\end{pmatrix})
Du coup la matrice de f dans la base
)
serait :
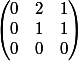
?
Salut,
quand on te donnes une application linéaire f et une base
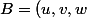)
et qu'on te demandes d'écrire la matrice de f dans la base B, la méthode est la suivante :
(1) on calcule f(u) f(v) et f(w)
(2) on exprime f(u) f(v) et f(w) en fonction de u,v et w. C'est-à-dire qu'on doit trouver des trucs de la forme
=a*u+b*v+c*w)
=d*u+e*v+f*w)
=g*u+h*v+i*w)
(3) on peut écrire la matrice de ton application linéaire f dans ta base B grâce a cette décomposition. On a donc:
=\quad<br />\begin{pmatrix} a&d &g\\b&e&h\\c&f&i\end{pmatrix})
Bref en revenant a ton exo, toi tu as calculé f(v1) tu trouves
= \begin{pmatrix}0\\0\\0\end{pmatrix}=0*v_1+0*v_2+0*v_3)
donc la première colonne de ta matrice dans la base (v1,v2,v3) sera constitué que de zéros.
Tu fais pareil pour f(v2) et f(v3) et tu auras ta matrice.
[De plus tu n'avais pas répondu a une partie de la première question qui disait d'exprimer
, f(v_2), f(v_3)) EN FONCTION DE
EN FONCTION DE 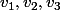
donc ça risquait pas d'être juste ....]


