équation du troisième degré
Olympiades mathématiques, énigmes et défis

-
yavlory
- Membre Relatif
- Messages: 133
- Enregistré le: 28 Nov 2017, 21:33
-
 par yavlory » 06 Fév 2018, 17:52
par yavlory » 06 Fév 2018, 17:52
Bonjour
pour éviter de polluer l'autre sujet
https://www.maths-forum.com/enigmes/autour-une-equation-troisieme-degre-t192329.html,
je propose l'énoncé suivant avec sa solution
et dans lequel on lève toute ambiguïté en faisant la différence entre
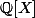
et
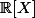 Enoncé Déterminer
Enoncé Déterminer l'ensemble
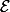
des polynômes
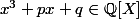
tel que
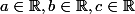
avec
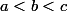
sont ses racines
et
exprimer 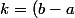 \in \mathbb {R})
et
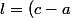\in \mathbb {R})
et qui sont les racines d'un polynôme
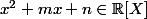 solution
solutionl'ensemble
\in \mathbb {Q}\times \mathbb {Q}\mid \exist p\in \mathbb {Q},p<0,\exist q\in \mathbb {Q},q\in ]t_1,t_2[, t_1= -\frac {2.\sqrt {-27p^3}}{27},t_2= \frac {2.\sqrt {-27p^3}}{27}\end {Bmatrix} \cup)
\in \mathbb {Q}\times \mathbb {Q}\mid \exist p\in \mathbb {Q},p<0,\exist q\in \mathbb {Q},q\in ]-u,u[,u =-\frac {\sqrt {-27p^3}}{27}\end {Bmatrix})
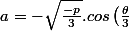-\sqrt {p.cos^2 \left( \frac {\theta}{3} \right)-p})
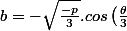+\sqrt {p.cos^2 \left( \frac {\theta}{3} \right)-p})
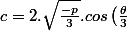)
avec l'angle géométrique
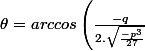)
on vérifie
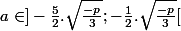
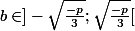
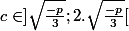
on obtient
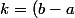 \in \mathbb {R})
et
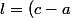\in \mathbb {R})
et qui sont les racines d'un polynôme
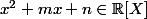
avec
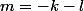
et
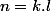

-
yavlory
- Membre Relatif
- Messages: 133
- Enregistré le: 28 Nov 2017, 21:33
-
 par yavlory » 06 Fév 2018, 18:48
par yavlory » 06 Fév 2018, 18:48
une faute corrigée
j'avais écris
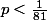
au lieu de
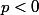
-
ordage
- Membre Naturel
- Messages: 13
- Enregistré le: 12 Déc 2017, 10:15
-
 par ordage » 08 Fév 2018, 12:28
par ordage » 08 Fév 2018, 12:28
yavlory a écrit:Bonjour
pour éviter de polluer l'autre sujet
https://www.maths-forum.com/enigmes/autour-une-equation-troisieme-degre-t192329.html,
je propose l'énoncé suivant avec sa solution
et dans lequel on lève toute ambiguïté en faisant la différence entre
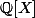
et
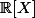 Enoncé Déterminer
Enoncé Déterminer l'ensemble
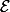
des polynômes
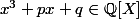
tel que
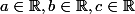
avec
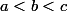
sont ses racines
et
exprimer 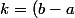 \in \mathbb {R})
et
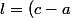\in \mathbb {R})
et qui sont les racines d'un polynôme
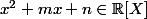 solution
solutionl'ensemble
\in \mathbb {Q}\times \mathbb {Q}\mid \exist p\in \mathbb {Q},p<0,\exist q\in \mathbb {Q},q\in ]t_1,t_2[, t_1= -\frac {2.\sqrt {-27p^3}}{27},t_2= \frac {2.\sqrt {-27p^3}}{27}\end {Bmatrix} \cup)
\in \mathbb {Q}\times \mathbb {Q}\mid \exist p\in \mathbb {Q},p<0,\exist q\in \mathbb {Q},q\in ]-u,u[,u =-\frac {\sqrt {-27p^3}}{27}\end {Bmatrix})
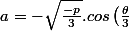-\sqrt {p.cos^2 \left( \frac {\theta}{3} \right)-p})
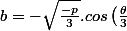+\sqrt {p.cos^2 \left( \frac {\theta}{3} \right)-p})
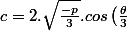)
avec l'angle géométrique
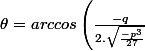)
on vérifie
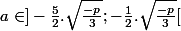
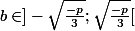
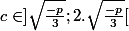
on obtient
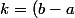 \in \mathbb {R})
et
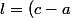\in \mathbb {R})
et qui sont les racines d'un polynôme
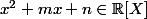
avec
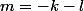
et
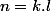
Bonjour
Merci pour ta proposition.
C'est bien le même résultat, que celui donné par Black Jack, établi plus formellement et plus pratique plus les calculs de (b-a) de (c-a) de (b-a)/(c-a), puisqu'on on a des simplifications même si le résultat reste assez compliqué.
Un point à souligner c'est que la solution ne dépendant que de la différence (b-a), (c-a) des racines, a, b, c de l'équation
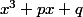
,
elle est aussi la solution de l'infinité d'équations dont les racines sont ( a +k), ( b+k), (c+k) ou k est une fonction scalaire dépendant des paramètres scalaires de l'équation (en fait p et q dépendent de 3 paramètres scalaires).
Est-ce correct?
Cordialement

-
yavlory
- Membre Relatif
- Messages: 133
- Enregistré le: 28 Nov 2017, 21:33
-
 par yavlory » 08 Fév 2018, 20:46
par yavlory » 08 Fév 2018, 20:46
Est-ce correct?
Bonjour Ordage
Je ne comprend pas trop votre question(c'est pour cela que j'ai ouvert ce sujet en posant une question mais la mienne afin de ne pas faire de hors sujet en répondant à votre question)
En fait je pense que j'ai mal compris le sujet que vous aviez ouvert et que finalement j'étais hors-sujet là-bas
je n'arrive pas à interpréter le sens que vous donnez au verbe 'dépendre'
mais bon si ce sujet là apporte un truc en plus c'est tant mieux mais j'ai fais ça un peu au hasard(et sans conviction)

-
yavlory
- Membre Relatif
- Messages: 133
- Enregistré le: 28 Nov 2017, 21:33
-
 par yavlory » 08 Fév 2018, 21:48
par yavlory » 08 Fév 2018, 21:48
...par exemple
si on me demande de quoi dépendent
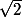
,
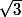
,
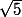
à la limite, je dirais au pif (au pif car je ne comprend pas la question)
non pas qu'ils dépendent des coefficients du polynôme
.\left(x-\sqrt {3}\right).\left(x-\sqrt {5}\right)\in \mathbb {R}[X])
les trois coefficients dans l'ordre déccroissant de l'exposant sur

associé au coefficient
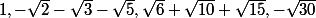
mais des coefficients de leurs polynômes minimaux respectifs(du second degré)
soit donc
les deux coefficients
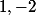
pour le polynôme
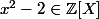
ayant
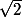
pour une de ses racines
les deux coefficients
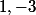
pour le polynôme
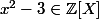
ayant
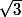
pour une de ses racines
les deux coefficients
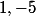
pour le polynôme
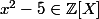
ayant
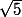
pour une de ses racines
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
