Spectre d'un opérateur

[sabeur]

Soit a>0, on considère, alors, l'opérateur de multiplication M: L^2(\omega)----> L^2(\omega) défini par M(f)=af.
A mon avis, le spectre associé à cet opérateur est le singleton {a}. Quelle est alors son spectre essentiel ? est - ce le vide ?

[aviateur]

Bonjour
Evidemment oui car (pour le spectre ponctuel) le seul élément qui n'est pas dans l'ensemble résolvant est a et a est une valeur propre.

[sabeur]

Merci pour votre réponse ...

Je veux, juste, savoir si la multiplicité de cette valeur propre n'est pas infinie car si non elle va-t-être dans le spectre essentiel ..

[aviateur]

Rebonjour
Il faut que l'on s'entende bien sur les définitions.
L'ensemble résolvant c'est l'ensemble des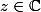 tel que (z-M) soit une bijection.
Et le spectre est son complémentaire.
Donc ={a}

Le spectre ponctuel est constitué des valeurs propres , ici a est une (la seule) valeur propre.

Le spectre essentiel est constitué des z tel que (z-M) n’est pas un opérateur de Fredholm d’indice 0. Ici (a-M) n'est pas un opérateur de Fredholm. Le spectre essentiel contient {a} selon cette définition .
Maintenant que vient faire la multiplicité? Et d'ailleurs c'est quoi la définition de la multiplicité?
Ici a est de multiplicité algébrique 1. non! de multiplicité algébrique et géométrique infini.

[marawita1]

@aviateur: Dans notre cours, mon prof. a défini le spectre essentiel comme étant l'ensemble des tel que est une valeur propre isolée de multiplicité infinie.
Pourquoi ici a est de multiplicité 1?

[aviateur]

Rebonjour J'ai modifié la réponse précédente à cause de ma mémoire qui a déconnée
En fait (a-M) n'est pas un opérateur de Fredholm et de plus la multiplicité algébrique de =multiplicité géométrique de a, car si on désigne par H l'espace L^2(Omega)


Quant à la définition de votre prof c'est possible car je sais qu'il y a plusieurs définitions concernant le spectre mais je ne les connais pas bien . Il faut voir aussi avec le spectre continu.

Je viens de voir quelque part que le spectre essentiel est la réunion du spectre continu et
et des valeurs propres z tel que Ker(z-M) est de dimension infini (cela correspond à la définition de votre prof).
Selon cette définition alors oui {a} est dans le spectre essentiel .
Donc la réponse selon la définition de votre prof maintenant coïncide avec la définition avec les opérateurs de Fredholm.

[marawita1]

Bonjour,
Merci bien aviateur pour vos explications.

[sabeur]

Bonjour

Si j'ai bien compris le spectre ponctuel est vide, non ?

[aviateur]

Bonjour
Non ici a est aussi dans le spectre ponctuel. Le spectre essentiel et le spectre ponctuel ne sont pas toujours disjoints.

[sabeur]

D'accord et merci beaucoup.