Aide exercice 1ere S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Ragy
- Messages: 3
- Enregistré le: 28 Oct 2017, 10:49
-
 par Ragy » 28 Oct 2017, 11:12
par Ragy » 28 Oct 2017, 11:12
Bonjour
J'ai besoin d'aide pour un exercice
Soit x et y deux réels positifs
1. Montrer que
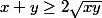
2. Si x et y sont des réels strictement positifs, déterminer le minimum du produit:
)
Merci

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 28 Oct 2017, 12:36
par capitaine nuggets » 28 Oct 2017, 12:36
Salut !
1. Avant tout, justifie que l'inégalité est bien définie. Ensuite, pense à l'identité remarquable
^2)
et utilise le fait que
^2 \ge 0)
. Précise le cas d'égalité également.
2. De la question précédente, tu en déduis que

et

. En précisant les cas d'égalité, déduis-en le minimum désiré.
-
Ragy
- Messages: 3
- Enregistré le: 28 Oct 2017, 10:49
-
 par Ragy » 28 Oct 2017, 17:43
par Ragy » 28 Oct 2017, 17:43
Tu peux me montrer comment tu as trouvé ta deuxième deduction s'il te plaît. Je n'arrive pas à la démontrer.
-
Ragy
- Messages: 3
- Enregistré le: 28 Oct 2017, 10:49
-
 par Ragy » 29 Oct 2017, 13:17
par Ragy » 29 Oct 2017, 13:17
Non c'est bon j'ai compris
Merci beaucoup!!!!!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 29 Oct 2017, 14:59
par Ben314 » 29 Oct 2017, 14:59
Salut,
Une façon un soupçon différente de procéder : si
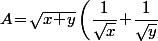)
alors
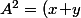\left(\dfrac{1}{x}\! +\!\dfrac{2}{\sqrt{xy}}\! +\!\dfrac{1}{y}\right)<br />=(x\!+\!y)\left(\dfrac{x\!+\!y}{xy}\! +\!\dfrac{2}{\sqrt{xy}}\right)<br />=t^2\!+\!2t\ \ \text{o\`u}\ \ t\!=\!\dfrac{x+y}{\sqrt{xy}})
Et il est clair que

(qui est positif) est minimum lorsque
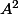
est minimum
et que

est minimum (avec

positif) lorsque

est minimum.
Or la question 1) dit que

(avec égalité ssi

)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités