Suite et limite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
lolo136
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2017, 08:12
-
 par lolo136 » 13 Oct 2017, 08:34
par lolo136 » 13 Oct 2017, 08:34
bonjour
Je dois trouver les limites de ces suites :
a)
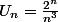
b)
^2}{\sqrt(n)})
c)
}}{n^{log(3)}})
pour la a j'ai dit que Un=(exp(nln2))/n^3 puis j'ai multiplié en haut et en bas par (ln2)^3 pour utiliser la formule des croissances comparées exp(x)/x^n tend vers l'infini quand x tend vers l'infini. donc Un tend vers l'infini.
Est-ce que c'est correct? Il y a plus simple ?
pour la b j'ai dit que c'était de la forme log(x)/x^a et donc d'après les croissances comparées ça tend vers 0
je sais pas si c'est bon parce que la on a du log et normalement la formule c'est avec ln
pour la c je ne sais pas du tout ..
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 13 Oct 2017, 09:07
par pascal16 » 13 Oct 2017, 09:07
log(a*b)=log(a)+log(b)
log(a^b)=b.log(a)
log = log en base 10
log(n) = ln(n)/ln(10)
pour la a : Un+1/Un tend vers combien ?, Un est-elle croissante ?
-
lolo136
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2017, 08:12
-
 par lolo136 » 13 Oct 2017, 09:18
par lolo136 » 13 Oct 2017, 09:18
Je trouve que ça tend vers 2 donc elle est croissante mais ça ne nous renseigne pas sur la limite
-
Tiruxa47
- Membre Relatif
- Messages: 343
- Enregistré le: 14 Jan 2017, 16:03
-
 par Tiruxa47 » 13 Oct 2017, 09:25
par Tiruxa47 » 13 Oct 2017, 09:25
Bonjour,
Pour la a) c'est correct, on pouvait aussi chercher la limite de Vn=ln Un mais pas sûr que ce soit plus simple,
on peut le faire aussi pour la c) (utiliser ln)
Pour la b) c'est le carré qui est plus génant que le log décimal, on peut chercher d'abord la limite Vn = racine carrée de Un..
-
lolo136
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2017, 08:12
-
 par lolo136 » 13 Oct 2017, 09:40
par lolo136 » 13 Oct 2017, 09:40
Pour la c j'ai :
}}{n^{log(3)}}=\frac{exp(log(n)*ln(2))}{exp(log(3)*ln(n)}=\frac{exp(ln(n)*ln(2)/ln(10))}{exp(ln(3)*ln(n)/ln(10)})
mais apres je ne sais pas trop
-
lolo136
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2017, 08:12
-
 par lolo136 » 13 Oct 2017, 09:41
par lolo136 » 13 Oct 2017, 09:41
pour la c on peut dire que Vn=log(n)/n^1/4 ce qui tend vers 0 d'après les croissances comparées
puis Un => Vn^2 => 0^2 tend aussi vers 0 ?
-
lolo136
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2017, 08:12
-
 par lolo136 » 13 Oct 2017, 11:53
par lolo136 » 13 Oct 2017, 11:53
Toujours bloqué...

-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 13 Oct 2017, 12:07
par pascal16 » 13 Oct 2017, 12:07
la a) version "je sais pas d'où ça sort".
Cherchons ce que vaut
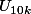
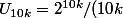^3)
2^10 = 1024 soit 1000 en gros
)
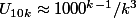
On pourrait conclure avec les croissances comparées des puissances et des exposants
et pour le k de la forme 10^p
)
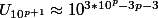
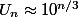
donc très grand
Modifié en dernier par
pascal16 le 13 Oct 2017, 20:23, modifié 1 fois.
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 13 Oct 2017, 12:23
par pascal16 » 13 Oct 2017, 12:23
pour la 3.
log(Un)=log(a/b) = log(a)-log(b)
log(2^log(n))=log(n)*log(2)
log(n^log(3))=log(3)*log(n)
log(Un)=log(n)*(log(2)-log(3))
Un=10^(log(n)*(log(2)-log(3)))
log(2)-log(3) est négatif, Un tends vers 0
-
lolo136
- Membre Naturel
- Messages: 14
- Enregistré le: 13 Oct 2017, 08:12
-
 par lolo136 » 16 Oct 2017, 08:27
par lolo136 » 16 Oct 2017, 08:27
Je vois merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités

