Demandes daide rapideLimites

[RENJIi4574]

bonjour jai un dm a rendre pour mardi je me casse la tete dessu depuis plus de deux heures et je narrive a rien je demande de laide juste pour me debloquer a chaque exercice je peut me debrouiller si on moriente bien merci



images completes https://www.devoirs.fr/terminale/mathem ... 15218.html

[infernaleur]

Moi j'arrive pas à voir l'image en entier.

[RENJIi4574]

Moi j'arrive pas à voir l'image en entier.

pareil ducoup jai mit sur dev.fr on la voi en entieres

[infernaleur]

Pour la première on te donne une inégalité pour f(x) sur R on a 1<=f(x)<=2. A partir de la tu trouve un encadrement pour g(x) sa devrait pas te poser de problème.

[RENJIi4574]

justement cest cette question qui mepose le plus de probleme la partit 2 si on me donne juste le nom de la proposition je pourrait me debrouiller et la partit 3 je les a peut pres comprit la grosse epines cest la partit 1

[infernaleur]

Il faut connaitre ses règles pour les inégalités et tu va voir c'est tout simple.
Soient a,b,c,k des réels
Si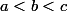 on a :
***
*** Si k est positif , si k est négatif on change le sens des inégalités

[RENJIi4574]

ducoup je part avec fx ou gx je bloque vraiment pourtant cest pas mon habitude je suis plutot bon en temp normal

[RENJIi4574]

cest bon jai trouver pour la question 1 en fait cetait assez simple une fois que lon part de f et que lon ajoute petit a petit ducoup si tu connait la proprieté de la partit 2 sa pourrait grandement maidé

[infernaleur]

moi au lycée on avait appelé cette propriété théorème de comparaison mais sa doit être dans ton cours .
Tu sais énoncé la réciproque de cette propriété ?

[RENJIi4574]

ouai jai dasnmon court la comparaison mais cest avec deux fonction fx et gx alors que la cest que x ducoup jhesite ausi avec le theroeme de majoration et de minoration par contre jai rien sur la reciproque ou en tout cas cest pas claire

[infernaleur]

Bha la fonction qui à x associe x c'est une fonction, on peux poser par exemple h(x)=x et on a donc f(x)<=h(x).
Qu'est ce qui dit ton théorème de majoration et de minoration ? (parce que c'est que des nom on apprend pas le même nom pour les théorèmes selon le lycée où on était )

[infernaleur]

la ta propriété est de la forme A => B la réciproque d'une telle propriété est tout simplement B=> A
Donc tu dois voir si lim f(x)=- l'infini est-ce que f(x) est forcément plus petit que x

[RENJIi4574]

normalement pour la reciproque je devraittrouver +infini
ducoup tu est sur pour la que cest comparaison et pas un autre ?

[infernaleur]

normalement pour la reciproque je devraittrouver +infini
ducoup tu est sur pour la que cest comparaison et pas un autre ?

Non pourquoi tu devrais trouver +l'infini ???
C'est pas sa une réciproque, je t'ai dit la réciproque de la propriété ;
Si f(x)<x alors lim f(x)=-linfini (pour x qui tend vers -l'infini)
C'est :
Si lim f(x)=-l'infini (pour x qui tend vers -l'infini) alors f(x)<x

[infernaleur]

normalement pour la reciproque je devraittrouver +infini
ducoup tu est sur pour la que cest comparaison et pas un autre ?

et je t'ai dit de m’énoncer tes théorème de majoration et de minoration peut être que c'est sa ....

[RENJIi4574]

normalement pour la reciproque je devraittrouver +infini
ducoup tu est sur pour la que cest comparaison et pas un autre ?

Non pourquoi tu devrais trouver +l'infini ???
C'est pas sa une réciproque, je t'ai dit la réciproque de la propriété ;
Si f(x)<x alors lim f(x)=-linfini (pour x qui tend vers -l'infini)
C'est :
Si lim f(x)=-l'infini (pour x qui tend vers -l'infini) alors f(x)<x

ducoup sa revient a redire la proposition non ?

[infernaleur]

normalement pour la reciproque je devraittrouver +infini
ducoup tu est sur pour la que cest comparaison et pas un autre ?

Non pourquoi tu devrais trouver +l'infini ???
C'est pas sa une réciproque, je t'ai dit la réciproque de la propriété ;
Si f(x)<x alors lim f(x)=-linfini (pour x qui tend vers -l'infini)
C'est :
Si lim f(x)=-l'infini (pour x qui tend vers -l'infini) alors f(x)<x

ducoup sa revient a redire la proposition non ?

Non la place des "Si" et des "Alors " jouent un rôle important.
Pour la première proposition on SUPPOSE que f(x)<x et on doit MONTRER si lim f(x)=-l'infini
Pour l'autre on SUPPOSE que lim f(x)=-l'infini et on doit MONTRER si f(x)<x

[infernaleur]

et pour théorème de majoration et de minoration si tu parle du théorème 1 de cette page http://www.wicky-math.fr.nf/pdf/2009-20 ... Limite.pdf. C'est bien sa.
Comme ta fonction est majorée par x sa sera le théorème de majoration.

[RENJIi4574]

et pour théorème de majoration et de minoration si tu parle du théorème 1 de cette page http://www.wicky-math.fr.nf/pdf/2009-20 ... Limite.pdf. C'est bien sa.
Comme ta fonction est majorée par x sa sera le théorème de majoration.

oui cest sa

[RENJIi4574]

ducoup je doit demontre par un calcul ?