Injectivité et surjectivité des fonctions par intervalle

[jankyjack]

Bonjour je voudrais trouver les valeurs de a (pas par la methode graphique) pour lesquelles la fonction suivante est injective et/ou surjective. j'ai essayé par la definition des deux mais je n'arrive à rien. je vous remercie de m'aider

[pascal16]

je pense que tu parles de R dans R

surjective :
première ligne
sur ]-oo;a[ que vaut I1=f(]-oo;a[ ) ?
sur [a;+oo[ il faut que I2=f([a;+oo[) soit tel que I1+I2=R (tu as le droit d'avoir des parties communes à I1 et I2)

Injective :
cette fois, il faut que I1 et I2 soient disjoints pour que personne n'ait 2 antécédents. et de plus
de ]-oo;a[ sur I1, f strictement croissante est injective
de [a;+oo[ sur I2, f doit être injective aussi, c'est à dire il faut que l'équation du second degré f(x)=z n'ai qu'une solution.
C'est plus dur car les deux conditions sur I2 sont liées.

[zygomatique]

salut

la fonction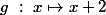 est strictement croissante sur donc sur 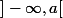et donc est une bijection de
]-oo, a[ sur ]-oo, f(a)[ avec f(a) = g(a) = a + 2

la fonction est strictement croissante sur [a, +oo[ et donc est une bijection de [a, +oo[ sur [fa), +oo[ avec

f est injective

f est surjective


on notera la cohérence qui conduit à : f est bijective (sur R)