Merci pour votre reponse
j'avais pas bien compris la question ^^ je l'ai fait mais maintenant je bloque à un encadrement d'integrale.. si vous pouvez m'aider

je vous recapitule l'exo avec les question si ca peut vous aider ( je suis à la 2b)
Soit F la fonction définie sur [1;+∞[ par:
= \int_{x}^{2x}{\frac{1}{ln(t)}}dt.)
1)a) Exprimer F à l'aide d'une primitive sur ]1;+∞[ de la fonction
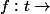
})
En déduire que F est dérivable sur ]1;+∞[
et que F'(x)=
(lnx)})
---> déja fait.
b) en deduire les sens de variations de F
---> decroissante sur ]1;2] et croissante sur [2;+∞[
2)a) Déterminer le sens de variation de f sur ]1;+∞[
-->decroissante sur ]1;+∞[
b) En deduire l'encadrement
}\leq F(x)\leq \frac{x}{ln(x)})
pour tout
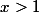
--> je bloque ici:
je sais que si pour tout x de [a;b] , f(x) < g(x) alors
} \leq \int_{a}^{b}{g(x)})
pour commencer, faut-il encadrer t de cette manière?
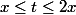
pour ensuite construire la fonction f? et prendre l'intégrale de chaque côté?
j'ai essayer ça:
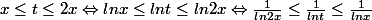
Donc:
\leq \int_{x}^{2x}{\frac{1}{lnx}})
je sais que c'est faux.. la question dit en déduire donc il faut déduire quelque chose de la variation de f sur ]1;+∞ [ parceque F'=f ?? et que dois-je en déduire pour trouver l'encadrement attendu?
Merci


