Nombres réel et sous-groupe additif de (R,+)

[medmed]

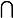
soit H un sous-groupe de (R,+) . On pose H+* = HR+* et =inf(H+*)
1-si H+* , montrer que H=Z
2-si n'appartient pas à H+* , montrer que =0 et en déduir que H est dense dans R

[zygomatique]

salut

si a > 0 alors soit y > a dans H+*

il existe un entier n tels que na =< y < (n + 1)a (car R est archimédien)

on en déduit alors que y - na < a

or .... et .... donc ....

[Kolis]

Bonsoir !
Il faut déjà être sûr de l'existence de : un ensemble vide n'a pas de borne inférieure.

@zygomatique t'a donné la solution pour 1.

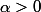
Pour 2., en supposant , tu montres qu'il y a un élément tel que .
Puis qu'il existe un élément . En considérant tu auras une contradiction!