Dérivée d'une composée de fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Bibi19
- Membre Naturel
- Messages: 16
- Enregistré le: 24 Fév 2016, 15:18
-
 par Bibi19 » 18 Oct 2016, 12:01
par Bibi19 » 18 Oct 2016, 12:01
Bonjour, j'ai un exercice à faire, je dois dérivée la fonction suivante :
 = \cos \left(\ln \sqrt{x^2+1} +5\right))
ce que j'ai fais :
 = -\sin \left(\ln \sqrt{x^2+1} +5\right) \times \frac{1}{\sqrt{x^2+1} } \times \frac{1}{2\sqrt{x^2+1}})
est ce correct ?
merci d'avance
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 18 Oct 2016, 12:22
par Pseuda » 18 Oct 2016, 12:22
Bibi19 a écrit:Bonjour, j'ai un exercice à faire, je dois dérivée la fonction suivante :
 = \cos \left(\ln \sqrt{x^2+1} +5\right))
ce que j'ai fais :
 = -\sin \left(\ln \sqrt{x^2+1} +5\right) \times \frac{1}{\sqrt{x^2+1} } \times \frac{1}{2\sqrt{x^2+1}})
est ce correct ?
merci d'avance
Bonjour,
Ce n'est pas exact. La dérivée de
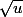
est

(tu n'as pas fait apparaître le u').
La dérivée de
)
est
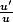
. Là encore, le u' n'apparaît pas dans ta formule.
-
Bibi19
- Membre Naturel
- Messages: 16
- Enregistré le: 24 Fév 2016, 15:18
-
 par Bibi19 » 18 Oct 2016, 14:22
par Bibi19 » 18 Oct 2016, 14:22
donc si je comprend bien, la dérivée sera :
 = -\sin \left(\ln \left(\sqrt{x^2+1} \right) +5\right) \times \frac{\frac{2x}{2\sqrt{x^2+1}}}\sqrt{x^2+1}{} \frac{} {})

-
siger
- Membre Complexe
- Messages: 2705
- Enregistré le: 16 Fév 2013, 19:56
-
 par siger » 18 Oct 2016, 15:05
par siger » 18 Oct 2016, 15:05
bonjour
pas encore!
f(x) = cos(ln (V(x²+1))+5)
ou
f(x) = cos (u) d'ou f'(x) = -u'*sinu
u(x) = ln(v)+5 d'ou u' = v'/v
v (x) = (x²+1)^(1/2) d'ou v' = x/(V(x²+1))
......
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 18 Oct 2016, 16:24
par Pseuda » 18 Oct 2016, 16:24
Bibi19 a écrit:donc si je comprend bien, la dérivée sera :
 = -\sin \left(\ln \left(\sqrt{x^2+1} \right) +5\right) \times \frac{\frac{2x}{2\sqrt{x^2+1}}}\sqrt{x^2+1}{} \frac{} {})

Bonsoir,
C'est ceci :
 = -\sin \left(\ln \left(\sqrt{x^2+1} \right) +5\right) \times \frac{1}\sqrt{x^2+1}{} \frac{} {})

On a :
' = \frac {u'}{u})
avec
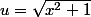
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 167 invités
 = -\sin \left(\ln \left(\sqrt{x^2+1} \right) +5\right) \times \frac{\frac{2x}{2\sqrt{x^2+1}}}\sqrt{x^2+1}{} \frac{} {})