Ensemble de points
16 messages
- Page 1 sur 1
Ensemble de points
Bonjour à tous !
Alors voilà, je rencontre un petit souci.
On me demande de déterminer l'ensemble suivant : E = { |z - 3+i| = | z barre + 2i | }
J'ai pensé à mettre une barre sur toute l'expression mais je n'aboutie à rien, merci de pouvoir m'aider!
Alors voilà, je rencontre un petit souci.
On me demande de déterminer l'ensemble suivant : E = { |z - 3+i| = | z barre + 2i | }
J'ai pensé à mettre une barre sur toute l'expression mais je n'aboutie à rien, merci de pouvoir m'aider!
Re: Ensemble de points
Salut
Si on ne voit rien du tout on peut toujours poser z=x+iy la forme algébrique et essayer de tirer des conséquences. Que penses-tu?
Si on ne voit rien du tout on peut toujours poser z=x+iy la forme algébrique et essayer de tirer des conséquences. Que penses-tu?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Ensemble de points
Merci de ta rapidité !
A vrai dire j'ai déjà essayé et ça m'a donné :
| (x+3) + i(y+1)| =| x + i( -y+2)|
Ca m'a l'air sans issue ..
A vrai dire j'ai déjà essayé et ça m'a donné :
| (x+3) + i(y+1)| =| x + i( -y+2)|
Ca m'a l'air sans issue ..
Re: Ensemble de points
Je vais mettre la main à la pâte avec toi. Essayons de voir si on calcule les modules au carré!
(X+3)^2 + (y+1)^2 = x^2 + (-y+2)^2
Et si tu passais tout d'un côté et qu'on essaye de factoriser...
(X+3)^2 + (y+1)^2 = x^2 + (-y+2)^2
Et si tu passais tout d'un côté et qu'on essaye de factoriser...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Ensemble de points
Tu vois un cercle toi? Moi je pense qu'on devrait tout simplifier d'abord avant de nous prononcer.
Equation d'un cercle serait x^2+y^2=r^2 mais là je vois pas encore cette forme..
Equation d'un cercle serait x^2+y^2=r^2 mais là je vois pas encore cette forme..
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Ensemble de points
c'est ce que me disais aussi mais j'ai passé tout d'un côté, je n'ai pas trouvé de facteur commun donc j'ai développé et simplifié et j'arrive à
-y^2 + 6y -6x +5 = 0
-y^2 + 6y -6x +5 = 0
Re: Ensemble de points
Il est pas normal qu'il te reste du y^2. Revois un peu
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Ensemble de points
Ah oui c'est vrai, tout est clair maintenant
Il reste 6y-6x+5 =0
6y = 6x-5
y = x -5/6
donc E est la droite d'équation y= x-5/6 \ {A(3, i) ; B(0, -2i)
est ce correct ?
Il reste 6y-6x+5 =0
6y = 6x-5
y = x -5/6
donc E est la droite d'équation y= x-5/6 \ {A(3, i) ; B(0, -2i)
est ce correct ?
Re: Ensemble de points
Euh c'est quoi ces points??? En plus pourquoi il y a i dans leurs coordonnées... xD comment tu places le point d'ordonnée i car perso c'est déjà dur de mesurer des rationnels sur la règle alors toi tu veux mesurer "i".
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Ensemble de points
si on prend z = 3+i on aura z barre + 2i =0 or c'est impossible
et si on prend z= 2i on aura aussi -3 + i = 0 ce qui est impossible donc il ne faut pas qu'ils appartiennent à la droite et le i dont tu parles c'est l'ordonnée dans le plan complexe car nous ne sommes pas dans un plan cartésien mais de toute façon ça ne change rien ce n'est qu'une notation
et si on prend z= 2i on aura aussi -3 + i = 0 ce qui est impossible donc il ne faut pas qu'ils appartiennent à la droite et le i dont tu parles c'est l'ordonnée dans le plan complexe car nous ne sommes pas dans un plan cartésien mais de toute façon ça ne change rien ce n'est qu'une notation
Re: Ensemble de points
salut
lorsqu'on sait qu'un nombre et son conjugué ont même module on en déduit que :
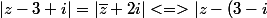| = |z - 2i|)
il suffit alors d'interpréter géométriquement le module d'un nombre complexe ... et de retourner au collège ...
lorsqu'on sait qu'un nombre et son conjugué ont même module on en déduit que :
il suffit alors d'interpréter géométriquement le module d'un nombre complexe ... et de retourner au collège ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Ensemble de points
Le collège ne nous a pas appris cela, par contre il nous a appris la réflexion en quelque sorte le respect.
et j'aimerais dire que l'on sait que |z| =|z barre| = |-z| mais là je ne vois pas le rapport
et j'aimerais dire que l'on sait que |z| =|z barre| = |-z| mais là je ne vois pas le rapport
Re: Ensemble de points
spiplat a écrit:Le collège ne nous a pas appris cela, par contre il nous a appris la réflexion en quelque sorte le respect.
MDR
zygomatique a écrit:salut
lorsqu'on sait qu'un nombre et son conjugué ont même module on en déduit que :
il suffit alors d'interpréter géométriquement le module d'un nombre complexe ... et de retourner au collège ...
et je retourne au collège pour reconnaître la médiatrice du segment [AB]
j'ai exactement suivi les indications qui m'ont été données avec respect sans aucun commentaire ni remarque ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Ensemble de points
D'ailleurs, pour faire le lien avec notre méthode
A(3;-1) et B(0;2)
(X-3)^2 + (y+1)^2 = x^2 + (-y+2)^2
<=> x^2 - 6x + 9 + y^2 + 2y + 1 = x^2 + y^2 - 4y + 4
<=> -6x + 10 + 2y = -4y + 4
<=> -6x + 6y + 6 = 0
<=> y = x-1
[AB] a pour milieu le point I(1.5;0.5) Et ce point appartient a notre droite !
(AB) a pour pente -1 donc notre droite coupe [AB] en son milieu et perpendiculairement. Donc c'est la médiatrice
A(3;-1) et B(0;2)
(X-3)^2 + (y+1)^2 = x^2 + (-y+2)^2
<=> x^2 - 6x + 9 + y^2 + 2y + 1 = x^2 + y^2 - 4y + 4
<=> -6x + 10 + 2y = -4y + 4
<=> -6x + 6y + 6 = 0
<=> y = x-1
[AB] a pour milieu le point I(1.5;0.5) Et ce point appartient a notre droite !
(AB) a pour pente -1 donc notre droite coupe [AB] en son milieu et perpendiculairement. Donc c'est la médiatrice
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
