Bonjour à tous
Lors de mes pérégrinations mathématiques syracusiennes, je suis arrivé à la récurrence suivante :
La suite doublement indexée
)
, où k et m sont des index entiers naturels vérifie :
=u(k,m)+\sum_{p=0}^{m}{\begin{pmatrix} m\\p \end{pmatrix}3^{p}u(k,p)})
avec les conditions initiales suivantes :
=0)
et
=2^{k})
. Je n'ai strictement aucune idée de la façon dont on pourrait déterminer l'expression du terme général de la suite
)
. Je suis preneur de toute suggestion.
Pour info,
)
, est le moment d'ordre m du reste de Terras, pris au rang k, c'est à dire
=\sum_{n=0}^{2^{k}-1}{\rho _{k,n}^{m}})
. Pour ceux qui ne connaissent pas, Terras a introduit la décomposition
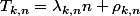
, où

est la k-ième itération de la fonction de Collatz compressée appliquée à n.
Je renvoie à son article Terras, Riho, A stopping time problem on the positive integers, Acta Arithmetica, Vol. 30, (1976), pp. 241 252, que l'on trouve dans toutes les bonnes librairies et tous les bons moteurs de recherche.
