Énoncé :
"Démonter par récurrence que pour tout entier naturel n >=1 :
1+(2*2!)+...+(n*n!)=(n+1)!-1"
J'ai donc prouvé que (P1) est vraie :
(1+1)!-1=1
Ensuite je m'attaque à la partie hérédité; d'un côté on a:
(n+3)!-1
et de l'autre:
(n+1)!-1 + [(n+1)*(n+1)!]
Il faut donc que je démontre que les deux sont égaux mais n'ayant jamais travaillé avec des factorielles je bloque dans mes calculs. Merci d'avance.
Recurrence
8 messages
- Page 1 sur 1
Re: Recurrence
Bonjour,
attention c'est (n+2)! -1 (au lieu de (n+3)!-1)
n! c'est 1*2*3*....*n donc
(n+1)! = (n+1)*n! et (n+2)! = (n+2)*(n+1)! ....
c'est clair pour toi ?
attention c'est (n+2)! -1 (au lieu de (n+3)!-1)
n! c'est 1*2*3*....*n donc
(n+1)! = (n+1)*n! et (n+2)! = (n+2)*(n+1)! ....
c'est clair pour toi ?
Re: Recurrence
salut
deux termes de la somme (n + 1)! - 1 + (n + 1)(n + 1)! ont un facteur commun ....
deux termes de la somme (n + 1)! - 1 + (n + 1)(n + 1)! ont un facteur commun ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Recurrence
Une fois tu as trouvé la solution par récurrence, tu pourrais jeter un coup d’œil à ça.
+&...&+&&(n*n!)\\S'_n=&1!+&2!+&3!+&4!+&\hdots+&n!\\S_n+S'_n=&2!+&3!+&...&+&n!&(n+1)!=-1+S'_{n+1}\\\end{matrix})
On obtiens donc:
 , de plus
, de plus 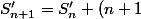! \Rightarrow S_n=(n+1)!-1)
On obtiens donc:
Re: Recurrence
Bonjour,
L'idée c'est de dire supposons que soit vraie. Ceci impliquerait il que
soit vraie. Ceci impliquerait il que 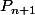 soit vraie.
soit vraie.
J'attire votre attention sur l'indice

L'idée c'est de dire supposons que
J'attire votre attention sur l'indice
Re: Recurrence
A titre d'exercice, vous pouvez poursuivre votre entrainement sur la récurrence en démontrant l'égalité suivante (c'était il y a pas longtemps ici même) :
superieur/utilisation-formule-binome-avec-racine-t176185.html#p1166067
superieur/utilisation-formule-binome-avec-racine-t176185.html#p1166067
Re: Recurrence
bolza a écrit:Bonjour,
attention c'est (n+2)! -1 (au lieu de (n+3)!-1)
n! c'est 1*2*3*....*n donc
(n+1)! = (n+1)*n! et (n+2)! = (n+2)*(n+1)! ....
c'est clair pour toi ?
Merci ça m'a beaucoup aidé! Je pense avoir réussi puisque je tombe sur n!*(n^2 + 3n + 2) -1.

Re: Recurrence
alors c'est bien triste ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
