Suite et arithmétique
27 messages
- Page 1 sur 2 - 1, 2
suite et arithmétique
salut
svp je n arrive pas à résoudre l exercice suivant et surtout la 2 em question
Soit la suite (un)n définie pour tout n par
U0=3 et un+1=2 (un)²-1
1)Montrer que un est divergente
2)Montrer que un+1 et un sont premiers entre eux
svp je n arrive pas à résoudre l exercice suivant et surtout la 2 em question
Soit la suite (un)n définie pour tout n par
U0=3 et un+1=2 (un)²-1
1)Montrer que un est divergente
2)Montrer que un+1 et un sont premiers entre eux
Re: suite et arithmétique
1) il suffit de montrer qu'elle est croissante et qu'elle n'admet pas de borne supérieure. Sinon il y a la possibilité de montrer que cette suite est minorée par une suite croissante et divergente (ce cas est facile à montrer).
Re: suite et arithmétique
2) A démontrer par l'absurde, suppose qu'il existe un diviseur commun......
Re: suite et arithmétique
Razes a écrit:Sinon il y a la possibilité de montrer que cette suite est minorée par une suite croissante et divergente (ce cas est facile à montrer).
Par exemple, j'ai montré qu'à partir de n = 2, on avait
C'est aussi vrai en n = 0 puis n = 1, mais l'hérédité ne veut passer que pour n>=2..tant pis pour elle ...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: suite et arithmétique
Qu'as-tu essayé de faire? La réponse ne tombera pas du ciel :p
As-tu suivi le conseil de Razes? Pour moi ça a marché !
As-tu suivi le conseil de Razes? Pour moi ça a marché !
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: suite et arithmétique
Même 'à partir de n = 1.Lostounet a écrit:Par exemple, j'ai montré qu'à partir de n = 2, on avait
P.S. Ne pas oublier la récurrence.
Si on te donne plus d'infos cela reviens à faire l'exercice à ta place. Un petit effort
Re: suite et arithmétique
Razes a écrit: Même 'à partir de n = 1.
Oui et même n = 0 mais je sais pas pourquoi
Serait-ce parce qu'il est temps d'aller dormir?

Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: suite et arithmétique
Razes a écrit:Tu as raison, c'est ce que je vais faire.
Bonne nuit à tous.
Je parlais de moi (car je dis pe des bêtises)


Mais il se fait tard et tu devrais aussi !
Et bonne nuit Yasmin

Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: suite et arithmétique
salut
2/ le théorème de Bézout donne immédiatement la réponse ...
2/ le théorème de Bézout donne immédiatement la réponse ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: suite et arithmétique
salut zygomatique
pour la question deux
(2un)un- un+1=1
a= 2 un et b=-1
ma question au niveau de l application du théorème de Bézout est ce qu il faut que a = 2 un ne dépend pas de n . c est a dire des entiers ne dépend pas de n
svp donner moi plus de détails
pour la question deux
(2un)un- un+1=1
a= 2 un et b=-1
ma question au niveau de l application du théorème de Bézout est ce qu il faut que a = 2 un ne dépend pas de n . c est a dire des entiers ne dépend pas de n
svp donner moi plus de détails
Re: suite et arithmétique
Hello,
 est toujours un entier car somme et produit d'entiers (par une récurrence immédiate...).
est toujours un entier car somme et produit d'entiers (par une récurrence immédiate...).
Le théorème de Bezout stipule que,
a et b sont premiers entre eux si et seulement si il existe deux entiers relatifs u et v tels que a·u + b·v = 1.
Soit n fixé dans N.
Ici, peux-tu mettre en jeu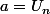 et
et 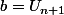 par ex?
par ex?
Le théorème de Bezout stipule que,
a et b sont premiers entre eux si et seulement si il existe deux entiers relatifs u et v tels que a·u + b·v = 1.
Soit n fixé dans N.
Ici, peux-tu mettre en jeu
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: suite et arithmétique
oui  est entier donc
est entier donc  \cdot u_n + (-1) \cdot u_{n + 1} = 1) est l'identité de Bézout ...
est l'identité de Bézout ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: suite et arithmétique
Salut zygomatique
merci pour votre réponse
mais si n n est pas fixé il y a un problème car dans le théorème Bézout qui prouve l existence de deux entier relatifs donc 2 un n est pas un entier alors car n varie
est qu on déterminer l expression du terme générale un
merci
merci pour votre réponse
mais si n n est pas fixé il y a un problème car dans le théorème Bézout qui prouve l existence de deux entier relatifs donc 2 un n est pas un entier alors car n varie
est qu on déterminer l expression du terme générale un
merci
Re: suite et arithmétique
ce que tu dis est incompréhensible ....
si on n'a plus d'entier alors il n'y a plus lieu de parler du théorème de Bézout ....
si on n'a plus d'entier alors il n'y a plus lieu de parler du théorème de Bézout ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: suite et arithmétique
YASMIN2016 a écrit:Salut zygomatique
merci pour votre réponse
mais si n n est pas fixé il y a un problème car dans le théorème Bézout qui prouve l existence de deux entier relatifs donc 2 un n est pas un entier alors car n varie
est qu on déterminer l expression du terme générale un
merci
Re: suite et arithmétique
Salut
si possible de trouver le terme générale (un) de cette suite et de l exprimer en fonction de n
merci
si possible de trouver le terme générale (un) de cette suite et de l exprimer en fonction de n
merci
Re: suite et arithmétique
Je ne pense pas.YASMIN2016 a écrit:Salut
si possible de trouver le terme générale (un) de cette suite et de l exprimer en fonction de n
merci
27 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
