Dérivée d'une fonction composée à la puissance n

[ralx]

Bonjour,
Connaît-on la dérivée de la fonction composée suivante f^n(u(x)).
C'est pour calculer l'intégrale de cos^n(u(x)) avec n une puissance donnée.
Il me semble que non mais je suis pas sûr.
Merci de m'éclairer.

[zygomatique]

salut

dérivée de f^n(x) ?

dérivée de f(u(x)) ?

[ralx]

Non la dérivée de comme par exemple .
Je suis peut-être plus clair comme ça.

[capitaine nuggets]

Salut !

Si on pose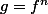 , alors donc .
Et que vaut ?

[ralx]

Merci. On a alors .

[zygomatique]

faux ...

[ralx]

Ah zut, pourtant j'ai vérifié avec et j'ai trouvé la même chose en utilisant la formule précédente et avec la dérivée du triple produit. J'ai trouvé .
Quelle est donc mon erreur ?

[capitaine nuggets]

Salut !

Si on pose , alors donc .
Et que vaut ?

Je pense que tu as mal écris ce que tu voulais dire : .

[ralx]

Oui c'est ce que je voulais dire. Voyons ce qu'en pense zygomatique.

[zygomatique]

si on ne veut pas se tromper il faut faire un effort d'écriture correcte :: f'(u(x)) n'est pas [f(u(x))]'