Unicité de fonction lipschitzienne

[monfort]

Bonjour,

Voici un problème intéressant dont je ne trouve pas la solution:
Soit non vide, et une fonction -lipschitzienne avec .
On suppose que est dense dans .
Montrer que l'on peut prolonger de façon unique tel que et avec

Toute suggestion est bienvenue!
Merci.

[Ben314]

Salut,

Soit non vide, et une fonction -lipschitzienne avec .
On suppose que est dense dans .
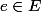
Montrer que l'on peut prolonger de façon unique tel que et avec Quel(s)

Pris tel quel, l'énoncé est clairement faux vu qu'il n'impose aucune condition sur à part éventuellement pour un (ou plusieurs ?) points de E.
De plus, il n'est pas clair vu que justement la variable qui apparait n'est pas quantifiée : est-ce "pour un certain fixé de E" ou bien "pour tout de E" ?
Sur ce deuxième point, je te charie un peu, vu que le terme "prolonger" du début de la phrase sous entend quand même pas mal que c'est "pour tout ", mais :
- Soit tu considère que ce "prolonge" veut, à lui seul dire, que et tu écrit rien d'autre.
- Soit tu considère que c'est pas clair ce que veut dire le "prolonge" et tu écrit complètement que , et pas en en oubliant la moitié.

[Ben314]

Sinon, en considérant que l'énoncé complet est :

Soit (*) et une fonction -lipschitzienne avec .
On suppose que est dense dans .
Montrer qu'il existe une unique aplication telle que :
1) soit -lipschitzienne.
2) (i.e. prolonge )

(*) "non vide" ne sert à rien : l'ensemble vide n'est évidement pas dense dans

Alors
- L'unicité découle immédiatement de la densité de E et de la continuité de : si deux fonctions continues qui sont égales sur un ensemble dense alors elle sont égale partout.
- Pour l'existence, c'est légèrement moins immédiat, mais, dans un espace complet, on peut utiliser...

[monfort]

Salut,
Je pense avoir bien réussi a montrer l'existence:
Soit suite de alors

[Ben314]

Soit suite de alors

Il me semble qu'il y a plus ou moins de bonnes idée, mais la façon de l'écrire est ABOMINABLE.
A mon avis, ce que tu voudrait dire, c'est que :
- On commence par prendre un x dans C.
- On considère ensuite une suite (Un) de E qui tend vers ce x là (possible vu que E est dense)
Alors que ce que tu as écrit, ça correspond à commencer par prendre une suite (Un) de E puis en déduire (c'est le sens du mot "alors" que tu as écrit) qu'elle converge vers un certain x. C'est évidement du "grand n'importe quoi"

Et concernant la suite, il y a éventuellement de l'idée, mais si je ne cherche pas à "lire entre les lignes" (ce que n'est pas sensé faire un correcteur d'examen...), j'aurais tendance à me demander quel est le rapport entre cette suite d'inégalité et la question posée.

[monfort]

Je vois. Il faudrait que je m'applique un peu plus en effet!
Merci beaucoup pour ton aide