Dérivations
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
E291076
- Messages: 5
- Enregistré le: 27 Déc 2015, 12:13
-
 par E291076 » 30 Déc 2015, 15:35
par E291076 » 30 Déc 2015, 15:35
Bonjour à tous, j'ai un exercice a faire mais je suis bloquer pour deux questions:
2) f est la fonction définie sur [40; 130] par f(x)= x² /290-x
a) Vérifier que f'(x)= -x(x-580)/(290-x)²
b) Prouver que f est croissante sur [40; 130]
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 30 Déc 2015, 15:48
par Carpate » 30 Déc 2015, 15:48
E291076 a écrit:Bonjour à tous, j'ai un exercice a faire mais je suis bloquer pour deux questions:
2) f est la fonction définie sur [40; 130] par f(x)= x² /290-x
a) Vérifier que f'(x)= -x(x-580)/(290-x)²
b) Prouver que f est croissante sur [40; 130]
Attention aux parenthèses !
 =\frac{x^2}{290-x})
est de la forme
}{v(x)})
et tu
dois connaître sa dérivée
u'(x)-u(x)v'(x)}{v^2(x)})
Alors, au boulot !
-
E291076
- Messages: 5
- Enregistré le: 27 Déc 2015, 12:13
-
 par E291076 » 30 Déc 2015, 15:52
par E291076 » 30 Déc 2015, 15:52
Carpate a écrit:Attention aux parenthèses !
 =\frac{x^2}{290-x})
est de la forme
}{v(x)})
et tu
dois connaître sa dérivée
u'(x)-u(x)v'(x)}{v^2(x)})
Alors, au boulot !
Oui, j'ai compris pour ça, je suis bloqué à 580x-x²/(290-x)²
je ne sais pas comment simplifier encore plus pour obtenir -x(x-580)/(290-x)²
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 30 Déc 2015, 15:57
par Carpate » 30 Déc 2015, 15:57
E291076 a écrit:Oui, j'ai compris pour ça, je suis bloqué à 580x-x²/(290-x)²
je ne sais pas comment simplifier encore plus pour obtenir -x(x-580)/(290-x)²
Tu n'étais pas loin :
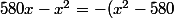=-x(x-580))
-
E291076
- Messages: 5
- Enregistré le: 27 Déc 2015, 12:13
-
 par E291076 » 30 Déc 2015, 16:17
par E291076 » 30 Déc 2015, 16:17
Carpate a écrit:Tu n'étais pas loin :
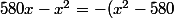=-x(x-580))
D'accord merci beaucoup et pour la question b faut-il faire un tableau signe ?
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 30 Déc 2015, 16:25
par titine » 30 Déc 2015, 16:25
E291076 a écrit:D'accord merci beaucoup et pour la question b faut-il faire un tableau signe ?
Si tu veux.
En fait pour montrer que f est croissante sur un intervalle il suffit de montrer que f'(x) est positif sur cet intervalle.
-
E291076
- Messages: 5
- Enregistré le: 27 Déc 2015, 12:13
-
 par E291076 » 30 Déc 2015, 16:32
par E291076 » 30 Déc 2015, 16:32
titine a écrit:Si tu veux.
En fait pour montrer que f est croissante sur un intervalle il suffit de montrer que f'(x) est positif sur cet intervalle.
Mais comment montrer que f'(x) est positif ?
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 30 Déc 2015, 17:00
par titine » 30 Déc 2015, 17:00
f'(x)= -x(x-580)/(290-x)²
Si x appartient à [40;130] :
-x est négatif
(x-580) est négatif
Donc -x(x-580) est posif.
De plus (290-x)² est positif (carré toujours positif)
Donc f'(x) est positif.
-
E291076
- Messages: 5
- Enregistré le: 27 Déc 2015, 12:13
-
 par E291076 » 30 Déc 2015, 17:38
par E291076 » 30 Déc 2015, 17:38
titine a écrit:f'(x)= -x(x-580)/(290-x)²
Si x appartient à [40;130] :
-x est négatif
(x-580) est négatif
Donc -x(x-580) est posif.
De plus (290-x)² est positif (carré toujours positif)
Donc f'(x) est positif.
Mais quel valeur on met entre 40 et 130 dans le tableau ?
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 30 Déc 2015, 17:50
par titine » 30 Déc 2015, 17:50
E291076 a écrit:Mais quel valeur on met entre 40 et 130 dans le tableau ?
Aucune.
Sur tout l'intervalle (40;130] la dérivée est positive.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
