Bonjour j'ai un exercice qui est
soit y=1/x pour x>0
soit M un poitn d'absicce a sur H ecrire en fonction de a l'équation de la tangente en m a H ca fait (-1/a²)x+2/a
la tangente en M coupe l'axes du répère en A et en B ecrire en fonction de a les coordonnée de A et de B et montrer que M milieu de [AB] quel que soit a merci de m'aider pour la derniere question
Dérivations
11 messages
- Page 1 sur 1
J'ai peut etre lu ton probleme un peu vite, mais comment as tu calculé les valeurs numériques des coordonnées des points ? Il me semble que tu devrai avoir leur expression en fonction de a. Une fois que tu as ca, M est le point d'abscisse a, tu n'as plus qu'a faire le calcul pour voir si c'est le milieu :)
Ah ok j'ai compris. Tu fais une confusion entre a est est l'abscisse du point M, c'est à dire que ses coordonnées sont M(a,f(a)) et x et y qui sont les abscisse et ordonnée dans ta fonction. Quand tu remplace dans ton équation de tangente, tu ne remplace pas le a qui lui est définie, tu remplace le x par 0 d'abord, puis ensuite le y. avec ca tu determine les coordonnées des points A et B. Essai de le faire et si tu n'as pas compris je t'écrirai un bout de solution pour que tu comprenne mieux, parce que je ne suis pas sur d'être très clair la ^^
Regarde : tu as l'équation de ta tangente : 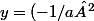x+2/a)
Maintenant tu cherche les deux point d'intersection avec les axes du repere, c-a-d le point A tel qu'il appartienne à l'axe des abscisse, c-a-d avec y=0.
En remplacant tu obtien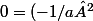x+2/a) et tu trouve la valeur de x (essai de le faire toi même).
et tu trouve la valeur de x (essai de le faire toi même).
Pour B c'est pareil, mais lui est l'intersection avec l'axe des ordonnées, c-a-d y=0. De même tu résoud l'équation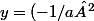*0+2/a=2/a) pour trouver x. Maintenant que tu as les coordonnées tu montre que M est le milieu de AB. As tu mieux compris?
pour trouver x. Maintenant que tu as les coordonnées tu montre que M est le milieu de AB. As tu mieux compris?
Maintenant tu cherche les deux point d'intersection avec les axes du repere, c-a-d le point A tel qu'il appartienne à l'axe des abscisse, c-a-d avec y=0.
En remplacant tu obtien
Pour B c'est pareil, mais lui est l'intersection avec l'axe des ordonnées, c-a-d y=0. De même tu résoud l'équation
la tangente en M coupe l'axes du répère en A et en B ecrire en fonction
de a les coordonnée de A et de B et montrer que M milieu de [AB] quel
que soit a merci de m'aider pour la derniere question
On sait que A est sur l'axe des abcisse d'où A(a',0)
B des ordonées d'où B(0,b)
de plus A et B sont sur la tangente a la courbe donc les coordonées respectent l'équation
y=f'(a)(x-a)+f(a)
y=(-1/a²)(x-a)+1/a
=(-1/a²)x+(2/a) (tu l'avais déja trouvé)
donc tu a :
Pour A: 0= (-1/a²)a'+2/a <=> -2/a(-a²)=a'<=> a'=2a donc A(2a,0)
Pour B: b= (-1/a²)*0+2/a <=> b=2/a donc B(0,2/a)
Les coordonées de M(x;y) milieu de [AB] sont :
x= (Xa+Xb)/2 = (2a+0)/2 = 2a/2 = a
y= (Ya+Yb)/2 = (0+2/a)/2 = 1/a
Or M a pour abscisse a et pour ordonnée f(a)=1/a, et la tu te dis que c'est magique!!!!!!
Donc pour tout a M est milieu de [AB]
de a les coordonnée de A et de B et montrer que M milieu de [AB] quel
que soit a merci de m'aider pour la derniere question
On sait que A est sur l'axe des abcisse d'où A(a',0)
B des ordonées d'où B(0,b)
de plus A et B sont sur la tangente a la courbe donc les coordonées respectent l'équation
y=f'(a)(x-a)+f(a)
y=(-1/a²)(x-a)+1/a
=(-1/a²)x+(2/a) (tu l'avais déja trouvé)
donc tu a :
Pour A: 0= (-1/a²)a'+2/a <=> -2/a(-a²)=a'<=> a'=2a donc A(2a,0)
Pour B: b= (-1/a²)*0+2/a <=> b=2/a donc B(0,2/a)
Les coordonées de M(x;y) milieu de [AB] sont :
x= (Xa+Xb)/2 = (2a+0)/2 = 2a/2 = a
y= (Ya+Yb)/2 = (0+2/a)/2 = 1/a
Or M a pour abscisse a et pour ordonnée f(a)=1/a, et la tu te dis que c'est magique!!!!!!
Donc pour tout a M est milieu de [AB]
dérivation...
bonjour... 2 méthodes:
1) Taux d'évolution en (a:1/a)
2) équation réduite de la tangente: y=mx+p m =f'(a) soit ici m=-1/a²... M sur la courbe , ses coordonnées vérifient l'équation de celle-ci ; on en déduit p=2/a d'où y=-1/a²x+2/a ; Quand y=0 on obtient l'abscisse en x'OX soit 2a.
Cqfd : Tracer une tangente à 1/x en a , il suffit de tracer la droite passant par M et le point sur X'OX de coordonnées (2a;0)
Pour ne pas faire d'erreur de signe dans les dérivées , utiliser plutôt la forme avec exposant (cela est beaucoup plus facile : y=1/X=X^(-1) y'=(-1)X^(-1-1)=-1/x²
soit f.générale: (U^n)'=nU'U^(n-1) s'entrainez pour retrouver toutes vos fonctions de base (ex: Vx=X^1/2) V racine "carré"
Bon weekend
bonjour... 2 méthodes:
1) Taux d'évolution en (a:1/a)
2) équation réduite de la tangente: y=mx+p m =f'(a) soit ici m=-1/a²... M sur la courbe , ses coordonnées vérifient l'équation de celle-ci ; on en déduit p=2/a d'où y=-1/a²x+2/a ; Quand y=0 on obtient l'abscisse en x'OX soit 2a.
Cqfd : Tracer une tangente à 1/x en a , il suffit de tracer la droite passant par M et le point sur X'OX de coordonnées (2a;0)
Pour ne pas faire d'erreur de signe dans les dérivées , utiliser plutôt la forme avec exposant (cela est beaucoup plus facile : y=1/X=X^(-1) y'=(-1)X^(-1-1)=-1/x²
soit f.générale: (U^n)'=nU'U^(n-1) s'entrainez pour retrouver toutes vos fonctions de base (ex: Vx=X^1/2) V racine "carré"
Bon weekend
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
