Calculé Un+1-Un

[ligator 31]

Bonjour à tous,
J'ai un devoir maison à faire, j'ai fais tous les exercices, cependant je but sur une question, celle de démontrer que Un est croissante en sachant que Un+1=e^(Un-1) , n =>0.
J'ai décidé de faire Un+1-Un et j'obtient donc : e^(Un-1) - Un , mais je ne parviens pas à résoudre ce calcul. Pouvez-vous m'aider ? :)
Merci d'avance et bonnes fêtes de fin d’année à tout le monde
Ligator 31

[Ben314]

Salut,
C'est vraiment ta formule ?
Ca signifie en fait qu'on a deux suites sans lien l'une avec l'autre : celle d'indices pairs et celle d'indice impairs.

Ou alors c'est ?

BILAN : met toi au MimeTeX...

EDIT : si ta formule est la deuxième, elle est de la forme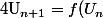 et pour savoir si est positif ou pas, ça semble pas trop bête d'étudier la fonction pour essayer d'en déduire son signe.

[ligator 31]

Bonjour ,
Merci pour ta réponse, en effet c'est bien la deuxième solution, dorénavant je vais utiliser le code ça évitera les erreurs, donc la suite c'est : .
Bonne soirée