je n'arrive pas à retrouver l'expression
Petit problème algébrique
6 messages
- Page 1 sur 1
petit problème algébrique
Bonjour,
je n'arrive pas à retrouver l'expression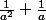 à partir de
à partir de 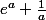 , est-ce d'ailleur possible avec ces informations ou ais-je besoin d'une fonction auxiliaire ? Merci d'avance pour votre aide
, est-ce d'ailleur possible avec ces informations ou ais-je besoin d'une fonction auxiliaire ? Merci d'avance pour votre aide
je n'arrive pas à retrouver l'expression
3,14 a écrit:C'est la dernière question d'un exercice: j'ai une fonction définie pardéfinie sur l'interval )0;+inf(. J'ai trouvé un minimum a dont la valeur est approchée à 0,7 (balayage). Je dois ensuite démontrer que f(a)=
.
Donc a vérifie f'(a) = 0.
C'est bien ça ?
Donc e^a - 1/a² = 0 (1) . D'accord ?
Je pense qu'en écrivant f(a) = e^a + 1/a et en utilisant la relation (1) tu dois t'en sortir
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 96 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
