Algorithme AlgoBox

[EazyE]

Bonjour à tous,

je dois faire cet exercice qui consiste à compléter et à améliorer un algorithme AlgoBox, mais malgré plusieurs essais infructueux, je n'arrive toujours pas à trouver la solution. J'ai même essayé de le faire avec un ami, mais même à deux on ne s'en sort pas. Est-ce quelqu'un pourrait m'aider à faire cet exercice, s'il vous plaît ?

D'avance merci

Liens vers l'énoncé :

http://imgur.com/ouuRg4U
http://imgur.com/pjO3M87

[Grimmys]

L'algorithmique est toujours très difficile à appréhender pour beaucoup d'élèves, alors que pour d'autres cela semble très intuitif oui. :/

Et malheureusement en occurrence l'exercice est extrêmement basique, c'est quelque chose du genre que tu pourras avoir au bac ( je le précise car à ta façon de dire " même avec un pote je n'ai pas réussi " on peut imaginer que tu considères l'exercice comme étant difficile de façon générale).

As tu déjà réussi à compléter les lignes masquées ?

[EazyE]

J'ai mis "S PREND_LA_VALEUR S + u" et "u PREND_LA_VALEUR u + r"

[Grimmys]

Bien, c'est correct.

Donc pour la 2 :

En fait, tu vois là qu'on a utilisé l'expression de (Un) sous sa forme de récurrence :



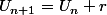
Et pour la somme, on a additionné aussi par étape jusqu'à la fin.


N'y a t-il pas plus simple ? Ne pouvons nous pas directement trouver la valeur de ?
Ne pouvons nous pas appliquer une formule permettant de calculer directement la somme des termes de la suite ?

Je pense que je viens de te donner bien assez d'indices pour conclure.

[EazyE]

J'ai trouvé cette formule dans le livre Sn = ((N + 1) * (u0 + un)) / 2, mais j'avoue que je n'arrive à représenter "un" sur AlgoBox. Cependant je ne retrouve jamais le même résultat qu'avec l'algorithme non-simplifié.

[Grimmys]

Avant de penser à comment réaliser la chose sur algobox, il faut que tu arrives à voir exactement ce que tu veux faire.

Tu possèdes une suite arithmétique de raison r connue et de premier terme aussi connu, comment peux tu l'écrire ?

[EazyE]

Je pense avoir réussi, les deux algorithmes donnent le même résultat. Merci beaucoup pour votre aide :++: .

Liens vers les algorithmes :

Non simplifié : http://imgur.com/tQwIuvl
Simplifié : http://imgur.com/TY4shS9