Deriver Fonction quotient o racine

[CanelleGEA]

Bonjour,
J'ai des devoirs a réaliser pour la rentrée en Mathématiques, je rencontre des difficultés à dériver des fonctions avec quotient plus racine par exemple : Sqrt(x/1-x) j'utilise donc (u'v-v'u)/2 ainsi que u'/2sqrt u, mais je n'y arrive toujours pas .. Ou encore sans racine mais avec quotient (2x-3/x)^3.. Serait il possible que l'on m'aide en me montrant l'acheminenment.. ?

[capitaine nuggets]

Salut !

Tu peux utiliser la formule donnant la dérivée d'une composée de deux fonctions :

[CENTER].[/CENTER]

Ensuite, pose tranquillement tes calculs :+++:
Si on note et alors :

[CENTER] [/CENTER]

(il faut juste que tu calcules au préalable et ).
Pour le second, utilise la formule de la dérivée d'une fonction élevée à une certaine puissance :

[CENTER].[/CENTER]

Ici, et 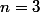. On a alors :

[CENTER][/CENTER]

(il faut juste que tu calcules au préalable ).
:++:

[CanelleGEA]

Merci bien pour votre réponse !! :we:
Cependant pour la premiere je ne comprends pas trop, cela donne ((1x-X-1)/(1-x)^2)*(1/2sqrt x)(x/1-X) ? Je ne comprends pas trop la formule :/

[capitaine nuggets]

Je pense que ton problème réside dans la compréhension de .

Calcule , puis remplace par dans l'expression de , cela te donnera alors l'expression de .

:we:

[CanelleGEA]

Ohhhhh merci beaucoup, j'ai enfin réussi, cela faisait 2 jours que j'étais sur cette fonction :mur: aha

[CanelleGEA]

Juste une dernière petite question(désolé) comment sais tu qui est f(x) et qui est g(x), comme ce n'est pas le numérateur et le dénominateur ?

[capitaine nuggets]

Juste une dernière petite question(désolé) comment sais tu qui est f(x) et qui est g(x), comme ce n'est pas le numérateur et le dénominateur ?

Je ne comprends pas bien ta question, pourrais-tu être plus précis(e) ?

[CanelleGEA]

Euh, en général avec la forme (u/v) u est le numérateur (x ici) et v le dénominateur (1-x) ici, pour f et g ca n'a pas l'air de marcher de la même façon ? (Je sais pas trop comment m'expliquer)

[capitaine nuggets]

Euh, en général avec la forme (u/v) u est le numérateur (x ici) et v le dénominateur (1-x) ici, pour f et g ca n'a pas l'air de marcher de la même façon ? (Je sais pas trop comment m'expliquer)

Oui, ici on a dérivé une fonction composée avec une autre et on a dérivé une puissance de fonction.

[mathelot]

Juste une dernière petite question(désolé) comment sais tu qui est f(x) et qui est g(x), comme ce n'est pas le numérateur et le dénominateur ?

la fontion à dériver

est la composée de


On dérive en sens inverse de la composition

[CanelleGEA]

Mais comment on reconnait une fonction composée ..?

[capitaine nuggets]

En fait, il est commode de recourir aux fonctions composées quand l'expression de semble trop compliquée pour être directement calculée.

Par exemple, pour calculer la dérivée de , il est préférable de poser où et . Puis on applique la formule de dérivation pour une composée de deux fonction.

Après, il n'y a pas de méthode unique pour calculer des dérivées.

:we:

[CanelleGEA]

D'accord , merci beaucoup d'avoir prit le temps, c'est vraiment gentil

[capitaine nuggets]

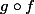Après je te rappelle que, pour deux fonctions et respectivement définies sur et tels que , on appelle composée de par la fonction notée définie sur par .

Attention, l'ordre a une importance : en général .

:+++:

[mathelot]

Imagine que tu dûsses dériver


l'application est la composée des applications:


on dérive en sens inverse des compositions,ie, le carré d'abord, puis le cosinus, puis la racine,puis la fraction,puis le cube .



Les nombres dérivés se multiplient et se calculent au même point que les fonctions:
par exemple la fraction se calcule ici en a=x^3

[CanelleGEA]

Merci :we: