Exercice Serie

par **Flo13** » 15 Juin 2015, 15:02

Bonjour voila lénoncé d'un esxercice de mon partiel de janvier en mathématique je n'y arrive pas. Merci d'avance pour votre aide.

Soit Un=ln(1+(-1)^n/n)

Trouver le plus petit entier n0 tel que Un0 est défini.
Démontrer que la serie \sum Un converge, et calculer sa somme.

par **Monsieur23** » 15 Juin 2015, 15:13

Aloha,

As-tu trouvé le n0 ?

Pour la convergence (et la somme), tu peux montrer que les deux suites de sommes partielles

et

convergent, vers la même limite.

par **Flo13** » 15 Juin 2015, 15:17

Salut, non; je suis sur ce partiel depuis 14h il y a 3 exercice et je n'y arrive pas du tout.

par **Monsieur23** » 15 Juin 2015, 15:22

Ben pour trouver n0, facile.

Essaye n=0. Si ça marche, alors n0=0. Sinon essaye n=1. Si ça marche, alors n0=1. Sinon

par **Flo13** » 15 Juin 2015, 15:27

OK donc si on prend n=0 on a Un=0 donc il est définit, après pour la convergence on peut la montrer avec la limite quand n->+infini ?

par **Monsieur23** » 15 Juin 2015, 15:28

Pour n=0, tu fais comment pour diviser (-1)^0 par 0 ?

par **Flo13** » 15 Juin 2015, 15:34

on peut pas mais vue que Un=ln(1+(-1)^0/0)=ln(1) non?

par **Monsieur23** » 15 Juin 2015, 15:36

Ben non. Si tu as une division par 0, c'est que ton truc il existe pas.

par **Flo13** » 15 Juin 2015, 15:38

d'accord donc donc faut n=2 car pour n=1 on a Un=ln(0) indéfini

par **Monsieur23** » 15 Juin 2015, 15:40

Ouais.

Ensuite, est-ce que tu sais calculer

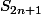
(où Sn est la suite des sommes partielles) ? Et

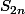
? Donc ?

par **Flo13** » 15 Juin 2015, 15:42

Pas du tout

par **Monsieur23** » 15 Juin 2015, 15:44

Je ne pense pas qu'en répondant en 2 minutes, tu aies essayé de faire le calcul bref.

Tu peux réécrire

. Avec cette formule , est-ce que tu peux calculer S2 ? S3? S4?

par **Flo13** » 15 Juin 2015, 15:54

S2= ln(3/2)
S3= ln(2/3)
S4= ln(5/4)

S2n+1= ln(1-1/(2n+1))

S2n = ln(1+1/2n)

par **zygomatique** » 15 Juin 2015, 16:03

salut

pour trouver n_0 on peut aussi résoudre l'inéquation

... qui est triviale ....

par **arnaud32** » 15 Juin 2015, 16:08

pour n=0 ou n=1 ca n'existe pas
pour

tu as

et

par **Monsieur23** » 15 Juin 2015, 22:05

Flo13 a écrit:S2= ln(3/2)
S3= ln(2/3)
S4= ln(5/4)

S2n+1= ln(1-1/(2n+1))

S2n = ln(1+1/2n)

Non, là tu as calculé U2, U3, U4

par **Flo13** » 16 Juin 2015, 19:47

Je ne vois pas peux tu m'expliquer?

par **Monsieur23** » 17 Juin 2015, 00:22

Ben ce que tu as calculé, ce sont les termes de la suite Un. Toi tu veux ceux de Sn.

Donc S2=U2, S3=U2+U3, S4=U2+U3+U4, etc.

par **Flo13** » 17 Juin 2015, 07:53

D'accord donc la suite tend vers 0 et elle converge. Il suffit de de calculé S2 S3 S4 pour le prouver ?

Exercice Serie

Exercice Serie

Qui est en ligne