Calcul
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
babygoodtn
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Nov 2007, 13:26
-
 par babygoodtn » 03 Juin 2015, 09:52
par babygoodtn » 03 Juin 2015, 09:52
S.V.P pourriez vous me faire ce calcul, parce que je galère
Soit
=\frac{u}{\sqrt{1+|u|^2}}\big( e^{-1+\sqrt{1+|z|^2}}-1\big))
Montrer que
|\leq C_\varepsilon |z|^2(e^{\varepsilon|z|^2}-1))
Je vous serai reconnaissant si vous me donner les détails du calcul.
-
DamX
- Membre Rationnel
- Messages: 630
- Enregistré le: 02 Oct 2012, 13:12
-
 par DamX » 03 Juin 2015, 13:47
par DamX » 03 Juin 2015, 13:47
Hello,
te faire le calcul non, t'aider peut-être, si tant est que l'énoncé est correct et complet.
C'est quoi le "u" dans ta première équation ?
pour l'inégalité à montrer, est-ce que c'est :
|\leq C_\varepsilon |z|^2(e^{\varepsilon|z|^2}-1))
?
enfin D est-elle la différentielle au sens réel, de la fonction complexe f à valeurs réelles ?
Damien
-
babygoodtn
- Membre Naturel
- Messages: 24
- Enregistré le: 23 Nov 2007, 13:26
-
 par babygoodtn » 03 Juin 2015, 15:58
par babygoodtn » 03 Juin 2015, 15:58
pour

et Df est la différentielle dans
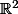
pour l'inégalité: oui pour tout

, il existe une constante C qui dépend de epsilon
A montrer:
|\leq C_\varepsilon |z|^2(e^{\varepsilon|z|^2}-1))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités