Equations trigonométrie 1ère S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
fly737
- Membre Naturel
- Messages: 30
- Enregistré le: 01 Mai 2014, 13:57
-
 par fly737 » 27 Fév 2015, 23:51
par fly737 » 27 Fév 2015, 23:51
Bonjour,
Je n'arrive pas à résoudre ces équations, pouvez vous m'aidez svp
Résoudre dans R les équations suivantes:
a) 2(cos x)^2 -1 = 2cos x.sin x
b) 2(sin x)^2 = 1
Merci d'avance !
-
mathelot
 par mathelot » 27 Fév 2015, 23:57
par mathelot » 27 Fév 2015, 23:57
bonsoir,
pour la (a),
)
et
)
s'écrivent avec
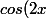)
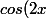=2cos^2(x)-1)
=2sin(x)cos(x))
pour la (b), calculer sin(x)
-
fly737
- Membre Naturel
- Messages: 30
- Enregistré le: 01 Mai 2014, 13:57
-
 par fly737 » 28 Fév 2015, 00:02
par fly737 » 28 Fév 2015, 00:02
Bonsoir,
Merci pour votre réponse,
Donc cela fait: Cos(2x)=Sin (2x) mais je ne vois pas comment développer svp
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 28 Fév 2015, 08:20
par Pisigma » 28 Fév 2015, 08:20
fly737 a écrit:Bonsoir,
Merci pour votre réponse,
Donc cela fait: Cos(2x)=Sin (2x) mais je ne vois pas comment développer svp
Bonjour,
Tu transformes le sin(2x) en cos(2x) ou le cos(2x) en sin(2x) et tu obtiens une égalité de cosinus ou de sinus.
-
mathelot
 par mathelot » 28 Fév 2015, 10:21
par mathelot » 28 Fév 2015, 10:21
=cos(2x)=sin(\frac{\pi}{2}-2x))
attention, ne pas oublier de diviser le modulo quand on divise les mesures d'angles par 4.
exemple:

-
fly737
- Membre Naturel
- Messages: 30
- Enregistré le: 01 Mai 2014, 13:57
-
 par fly737 » 28 Fév 2015, 12:33
par fly737 » 28 Fév 2015, 12:33
Merci mais pourquoi sin2x=cos2x=sin(pi/2-2x) ?
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 28 Fév 2015, 12:59
par Pisigma » 28 Fév 2015, 12:59
fly737 a écrit:Merci mais pourquoi sin2x=cos2x=sin(pi/2-2x) ?
C'est une formule que tu dois sûrement connaître.
Quand deux angles sont complémentaires (=leur somme vaut

à
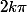
près)
=sin(\frac{\pi}{2}-x))
-
mathelot
 par mathelot » 28 Fév 2015, 13:07
par mathelot » 28 Fév 2015, 13:07
-
fly737
- Membre Naturel
- Messages: 30
- Enregistré le: 01 Mai 2014, 13:57
-
 par fly737 » 28 Fév 2015, 15:05
par fly737 » 28 Fév 2015, 15:05
Merci mais dans ce cas là, si Cos (2x)=Sin(2x)=Sin (pi/2 -2x) alors l'équation devient:
Sin (pi/2 -2x)=Sin (pi/2 -2x) ?
-
mathelot
 par mathelot » 28 Fév 2015, 15:09
par mathelot » 28 Fév 2015, 15:09
elle devient
=sin(\frac{\pi}{2}-2x))
nous avons deux abscisses curvilignes (en radian pour fixer les idées)
qui ont même sinus.
On obtient deux cas, deux points sur le cercle de part et d'autre de l'axe y'Oy,
deux points qui ont même ordonnée cartésienne.
-
fly737
- Membre Naturel
- Messages: 30
- Enregistré le: 01 Mai 2014, 13:57
-
 par fly737 » 28 Fév 2015, 15:13
par fly737 » 28 Fév 2015, 15:13
Mais normalement Sin (2x)= Cos (pi/2 -2x) ?
-
mathelot
 par mathelot » 28 Fév 2015, 16:01
par mathelot » 28 Fév 2015, 16:01
vous confondez les identités et les équations. :doh:
pour tout x
=cos(\frac{\pi}{2}-x))
est une identité
pour quelques x à déterminer:
cos(2x)=sin(2x) est une équation
-
fly737
- Membre Naturel
- Messages: 30
- Enregistré le: 01 Mai 2014, 13:57
-
 par fly737 » 28 Fév 2015, 16:32
par fly737 » 28 Fév 2015, 16:32
Merci mais c'est la différence ? (Dsl)
-
mathelot
 par mathelot » 28 Fév 2015, 17:07
par mathelot » 28 Fév 2015, 17:07
l'équation est
=sin(\frac{\pi}{2}-2x))
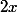
et

ont même sinus.
les angles sont égaux ou supplémentaires.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités

