Trajectoires orthogonales (dérivée implicite)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par GuillaumeDrolet » 27 Fév 2015, 23:13
par GuillaumeDrolet » 27 Fév 2015, 23:13
Bonsoir
Je dois démontrer que

et

sont orthogonales en utilisant la dérivation implicite et je ne vois pas comment.
Merci

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Fév 2015, 00:54
par zygomatique » 28 Fév 2015, 00:54
salut
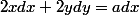
donc
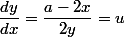
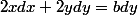
donc
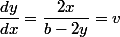
or les points d'intersection de ces courbes ont pour coordonnées
)
car ax = by
donc
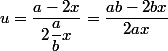
et

damned le produit uv devrait faire -1 ....
un vecteur normal est
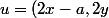)
un vecteur normal est
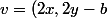)
leur produit scalaire est
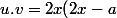 + 2y(2y - b) = 4x^2 + 4y^2 - 2ax - 2by = 0)
donc ces courbes sont orthogonales
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
 par GuillaumeDrolet » 28 Fév 2015, 04:30
par GuillaumeDrolet » 28 Fév 2015, 04:30
OK je comprend la dérivée implicite au début (quoi que est-ce que vous pourriez expliquer en quoi elle aide a déterminer si les courbes sont orthogonales?...)
Mais à partir du moment où vous parlez du produit de u et v je suis perdu. Je ne comprend pas vraiment le but de faire un produit scalaire ni d'où tous ces chiffres sortent [
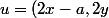)
et
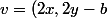)
] et pourquoi
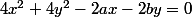
prouve qu'ils sont orthogonales.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 28 Fév 2015, 10:13
par zygomatique » 28 Fév 2015, 10:13
prenons alors simplement une droite d'équation ax + by + c = 0
alors un vecteur normal est (a, b) que l'on obtient en différentiant implicitement ....
or ::
deux courbes sont orthogonales en un point <=> les tangentes sont perpendiculaires <=> leurs vecteurs directeurs sont orthogonaux <=> leurs vecteurs normaux sont orthogonaux
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 28 Fév 2015, 11:37
par chan79 » 28 Fév 2015, 11:37
salut
C'est un peu lourd comme calcul mais on peut obtenir les équations des courbes orthogonales:
on part de

on dérive
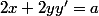
on multiplie par

et on remplace
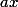
par
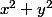
et
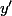
par

on obtient l'équation différentielle:
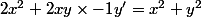
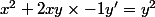
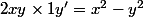
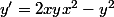
Comme cette équation est homogène, on pose
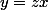
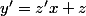
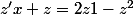
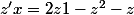

dz}{z+z^3}=\fra{dx}{x})
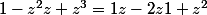
donc
=ln(kx))

on remplace

par

on obtient
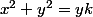
en posant
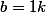

il y a sans doute plus simple
cette méthode marche avec beaucoup de familles de courbes
Tout cercle rouge se coupe "à angles droits" avec tout cercle bleu.
cercles rouges:x²+y²=ax
cercles bleus:x²+y²=by

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
