Series de fourier
23 messages
- Page 1 sur 2 - 1, 2
Series de fourier
Salut ,
j'ai besoin d'aide dans cet exercice qui porte sur les series de fourier :
f(x)=pi-x si x appartient à[0,pi]
0 si x appartient à[pi,2pi]
j'ai besoin de vérification pour les coefficients de fourier , j'ai trouvé :
a0=pi/4 , a2n=0 , a2n+1=2/(pi*n^2) et bn=1/n .
Et puis pour la 3éme question on me demande de determiner la somme S de la serie . Est-ce que je dois etudier la convergence de la serie et determiner f(x) ?
Merci d'avance.
j'ai besoin d'aide dans cet exercice qui porte sur les series de fourier :
f(x)=pi-x si x appartient à[0,pi]
0 si x appartient à[pi,2pi]
j'ai besoin de vérification pour les coefficients de fourier , j'ai trouvé :
a0=pi/4 , a2n=0 , a2n+1=2/(pi*n^2) et bn=1/n .
Et puis pour la 3éme question on me demande de determiner la somme S de la serie . Est-ce que je dois etudier la convergence de la serie et determiner f(x) ?
Merci d'avance.
Someday a écrit:Salut ,
j'ai besoin d'aide dans cet exercice qui porte sur les series de fourier :
f(x)=pi-x si x appartient à[0,pi]
0 si x appartient à[pi,2pi]
j'ai besoin de vérification pour les coefficients de fourier , j'ai trouvé :
a0=pi/4 , a2n=0 , a2n+1=2/(pi*n^2) et bn=1/n .
Et puis pour la 3éme question on me demande de determiner la somme S de la serie . Est-ce que je dois etudier la convergence de la serie et determiner f(x) ?
Merci d'avance.
Salut, cela a l'air juste, j'ai trouvé les mêmes coefficients.
Oui, cela semble cela.
Je pense que ta fonction n'est ni paire ni impaire et -périodique, donc ,
-périodique, donc ,  ,
, dt) ,
, f(t) dt) et
et f(t) dt.)
On obtient , puis,
, puis, 
, a_{2p+1}=\frac{2}{\pi(2p+1)^2}) et
et  ; donc sauf pour
; donc sauf pour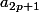 où tu n'élèves pas au carré
où tu n'élèves pas au carré ) , cest bon.
, cest bon.
En ce qui concerne la convergence, f vérifie les conditions de Dirichlet (f admet sur une période un seul point de discontinuité simple puisque=0) et
et=\pi) existent)
existent)
Par conséquent (théorème de Dirichlet) si t n'est pas un point de discontinuité;
+b_nsin(nt)=f(t)) et si
et si  est un point de discontinuité,
est un point de discontinuité,
+b_nsin(nt)=\frac{1}{2}(f(t_0-)+f(t_0+))=\frac{\pi}{2})
Petit complément: puisque f est discontinue en 0, que sin(0)=0 et cos(0)=1, on obtient:
^2}=\frac{\pi}{2})
^2}=\frac{\pi}{4})
^2}=\frac{(\pi)^2}{8})
La limite de cette série convergente n'est pas facile à trouver autrement! Et en prime un petit programme pour vérifier!
1 VARIABLES
2 N EST_DU_TYPE NOMBRE
3 p EST_DU_TYPE NOMBRE
4 S EST_DU_TYPE NOMBRE
5 DEBUT_ALGORITHME
6 LIRE N
7 S PREND_LA_VALEUR 0
8 POUR p ALLANT_DE 0 A N
9 DEBUT_POUR
10 S PREND_LA_VALEUR S+1/pow(2*p+1,2)
11 FIN_POUR
12 AFFICHERCALCUL Math.PI*Math.PI/8
13 AFFICHER "S="
On obtient
En ce qui concerne la convergence, f vérifie les conditions de Dirichlet (f admet sur une période un seul point de discontinuité simple puisque
Par conséquent (théorème de Dirichlet) si t n'est pas un point de discontinuité;
Petit complément: puisque f est discontinue en 0, que sin(0)=0 et cos(0)=1, on obtient:
La limite de cette série convergente n'est pas facile à trouver autrement! Et en prime un petit programme pour vérifier!
1 VARIABLES
2 N EST_DU_TYPE NOMBRE
3 p EST_DU_TYPE NOMBRE
4 S EST_DU_TYPE NOMBRE
5 DEBUT_ALGORITHME
6 LIRE N
7 S PREND_LA_VALEUR 0
8 POUR p ALLANT_DE 0 A N
9 DEBUT_POUR
10 S PREND_LA_VALEUR S+1/pow(2*p+1,2)
11 FIN_POUR
12 AFFICHERCALCUL Math.PI*Math.PI/8
13 AFFICHER "S="
Someday a écrit:Salut ,
j'ai besoin d'aide dans cet exercice qui porte sur les series de fourier :
f(x)=pi-x si x appartient à[0,pi]
0 si x appartient à[pi,2pi]
j'ai besoin de vérification pour les coefficients de fourier , j'ai trouvé :
a0=pi/4 , a2n=0 , a2n+1=2/(pi*n^2) et bn=1/n .
Et puis pour la 3éme question on me demande de determiner la somme S de la serie . Est-ce que je dois etudier la convergence de la serie et determiner f(x) ?
Merci d'avance.
Bonjour, en faisant les calculs :
En utilisant :
On alors alors
D'où
D'où
Donc attention à bien remplacer ton
On alors aussi
paquito a écrit:Je pense que ta fonction n'est ni paire ni impaire et-périodique, donc ,
,
,
et
On obtient, puis,
et
; donc sauf pour
où tu n'élèves pas au carré
, cest bon.
En ce qui concerne la convergence, f vérifie les conditions de Dirichlet (f admet sur une période un seul point de discontinuité simple puisqueet
existent)
Par conséquent (théorème de Dirichlet) si t n'est pas un point de discontinuité;et si
est un point de discontinuité,
Petit complément: puisque f est discontinue en 0, que sin(0)=0 et cos(0)=1, on obtient:^2}=\frac{\pi}{4})
La limite de cette série convergente n'est pas facile à trouver autrement! Et en prime un petit programme pour vérifier!
1 VARIABLES
2 N EST_DU_TYPE NOMBRE
3 p EST_DU_TYPE NOMBRE
4 S EST_DU_TYPE NOMBRE
5 DEBUT_ALGORITHME
6 LIRE N
7 S PREND_LA_VALEUR 0
8 POUR p ALLANT_DE 0 A N
9 DEBUT_POUR
10 S PREND_LA_VALEUR S+1/pow(2*p+1,2)
11 FIN_POUR
12 AFFICHERCALCUL Math.PI*Math.PI/8
13 AFFICHER "S="
Exactement dans la suite de l'exercice on me demande calculer cette somme là et puis de deduire la somme de 1/n^2 qui que j'ai trouvé (pi)^2/6 .
Someday a écrit:Exactement dans la suite de l'exercice on me demande calculer cette somme là et puis de deduire la somme de 1/n^2 qui que j'ai trouvé (pi)^2/6 .
C'est bon! La dernière somme S s'obtient en observant que
Probleme serie de fourier
Bonjour à tous !
Alors voilà j'ai un exercice sur les series de fourier:
voilà l'énoncé :
fonction périodique de PI et égale à f(t)=sin(2t) sur l'intervalle 0 ; PI
sagit-il d'une fonction impaire ?
Et de même pour un autre énoncé :
fonction f(t)= 3t-2 quand 0
(celle ci je pense que que ce n'est ni l'un, ni l'autre).
Alors voilà j'ai un exercice sur les series de fourier:
voilà l'énoncé :
fonction périodique de PI et égale à f(t)=sin(2t) sur l'intervalle 0 ; PI
sagit-il d'une fonction impaire ?
Et de même pour un autre énoncé :
fonction f(t)= 3t-2 quand 0
(celle ci je pense que que ce n'est ni l'un, ni l'autre).
merci paquito.
Donc a0, an, b0 et bn valent tous 0 ?? :hein:
au fait pardon, j'ai pas préciser la période pour le 2nd énoncé : période de 2 et l'énoncé dit que c'est paire. (encore désolé)
pour ce qui est de l'intégration par partie dont tu parle, comment en faire une, sachant que l'on a juste une seul définition pour 0
Donc a0, an, b0 et bn valent tous 0 ?? :hein:
au fait pardon, j'ai pas préciser la période pour le 2nd énoncé : période de 2 et l'énoncé dit que c'est paire. (encore désolé)
pour ce qui est de l'intégration par partie dont tu parle, comment en faire une, sachant que l'on a juste une seul définition pour 0
pour le (an) de la fonction f(t)=3t-2 sur 0
je trouve an=(-6^n)/(pi²*n²)
sauf que l'orsque l'on remplace n par 0, on ne trouve pas -0.5 (comme prévu), mais 0.
suis-je sur la bonne voie ?
j'ai fait lintégration par partie de:
(4/T)* [INTEGRALE de (T/2) à 0] de f(t)cos(nwt)
donc : (4/2)* [INTEGRALE de (2/2) à 0] de (3t-2)cos(n*(pi)*t)
je trouve an=(-6^n)/(pi²*n²)
sauf que l'orsque l'on remplace n par 0, on ne trouve pas -0.5 (comme prévu), mais 0.
suis-je sur la bonne voie ?
j'ai fait lintégration par partie de:
(4/T)* [INTEGRALE de (T/2) à 0] de f(t)cos(nwt)
donc : (4/2)* [INTEGRALE de (2/2) à 0] de (3t-2)cos(n*(pi)*t)
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
