Carlomath a écrit:Bonjour,
Je me suis intéressé à la suite récurrente définie par :
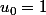
et
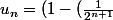})u_{n-1})
pour tout
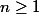
. Autrement dit, on peut écrire la suite de cette façon :

et pour tout
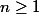
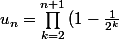})
Il est évident que cette suite converge (décroissante et minorée par 0), mais est-il possible de déterminer sa limite ? J'ai essayé, mais sans succès...
Cette suite m'intéresse car j'ai remarqué à la calculatrice que sa limite est étonnamment proche de la constante d'Euler-Mascheroni (0,577...).
Si vous avez des suggestions ou des pistes, merci beaucoup

Salut,
Dommage, ça aurait pu être sympa de trouver cette limite mais...
Au départ, j'ai cherché un moyen de l'expliciter, je n'y suis pas encore arrivé.
Après je me suis dit : mais si je dois montrer que c'est effectivement cette constante, j'ai intérêt à trouver les séries qui permettent de la retrouver.
Cependant, rien...
Alors, j'ai de nouveau regardé la calculatrice, calculé avec un algo de rien du tout un terme assez loin.
Pour finir par voir que la limite de ta série est

, super proche de la constante

.
Bon c'est qu'une conjecture, mais suffit de regarder les valeurs.
Je te montre le chemin que j'ai testé.
Après avoir essayé de manipuler le produit, sans succès, je me suis attelé à regarder ce que ça donnerait avec les transformées en Z.
Ta suite est définie par
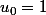
et
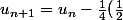^n u_n)
si je n'ai pas fait d'erreur.
Zu la transformée de u en z devient solution de l'équation fonctionnelle (après calculs) :
(z) \times (z-1) = z - \frac{1}{4} (Zu)(2z))
D'après le théorème de la valeur finale, il suffit de calculer la limite
(z) \times (z-1))
quand

qui est la limite de

en l'infini, ce que nous cherchons.
Donc il s'agit de trouver la limite de
(2z))
en 1.
Le hic, c'est que je n'arrive pas à expliciter la transformée, notamment car on prend la fonction en 2z...
Alors peut-être que quelqu'un peut nous donner un coup pour trouver cette transformée et conclure.
Quoi qu'il en soit, c'est un chemin...
