Etude de courbe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
adrien17
- Messages: 5
- Enregistré le: 11 Jan 2015, 13:56
-
 par adrien17 » 31 Jan 2015, 15:53
par adrien17 » 31 Jan 2015, 15:53
Bonjour,
J'ai un Dm de maths qui me pose quelques problèmes depuis 3 jours, je viens donc chercher de l'aide ici.
Soit la fonction f définie sur [-3;+  [
[
f(x) = (x² + 4x - 4)/(x² -2x +2)
On note C la courbe représentative de f.
1) Vérifiez que f est bien définie sur [-3;+;)[
2) Montrez que pour tout réel x  -3,
-3,
f(x) -1 = (6(x-1))/(x²-2x+2)
Préciser la position de C par rapport à la droite D d'équiation y=1
3) Montrez que pour tout réel x  3,
3,
f'(x) = (-6x²+12x)/((x²-2x+2)²)
En déduire les variations de f sur [-3; +;)[Mes réponses :
1) f est définie quand x²-2x+2 est différent de 0
x²-2x+2 = 0

= -4 a>0
f étant définie sur R, elle est aussi définie sur [-3; +;)[
2) C'est là que je bloque... J'ai cherché à simplifier (x²+4x-4)/(x²-2x+2) -1 mais je trouve (2x -) / (x²-x+), donc je pense avoir fait une erreur quelque part. Je n'arrive malheureusement pas à la trover, j'espère obtenir de l'aide ici !
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 31 Jan 2015, 16:07
par Carpate » 31 Jan 2015, 16:07
adrien17 a écrit:Bonjour,
J'ai un Dm de maths qui me pose quelques problèmes depuis 3 jours, je viens donc chercher de l'aide ici.
Soit la fonction f définie sur [-3;+  [
[
f(x) = (x² + 4x - 4)/(x² -2x +2)
On note C la courbe représentative de f.
1) Vérifiez que f est bien définie sur [-3;+;)[
2) Montrez que pour tout réel x  -3,
-3,
f(x) -1 = (6(x-1))/(x²-2x+2)
Préciser la position de C par rapport à la droite D d'équiation y=1
3) Montrez que pour tout réel x  3,
3,
f'(x) = (-6x²+12x)/((x²-2x+2)²)
En déduire les variations de f sur [-3; +;)[Mes réponses :
1) f est définie quand x²-2x+2 est différent de 0
x²-2x+2 = 0

= -4 a>0
f étant définie sur R, elle est aussi définie sur [-3; +;)[
2) C'est là que je bloque... J'ai cherché à simplifier (x²+4x-4)/(x²-2x+2) -1 mais je trouve (2x -) / (x²-x+), donc je pense avoir fait une erreur quelque part. Je n'arrive malheureusement pas à la trover, j'espère obtenir de l'aide ici !
Pour faire apparaître le 1, il faut faire apparaître le dénominateur :
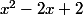
dans l'expression du dénominateur :

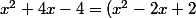 +6x -6=(x^2-2x+2) +6(x -1))
-
adrien17
- Messages: 5
- Enregistré le: 11 Jan 2015, 13:56
-
 par adrien17 » 31 Jan 2015, 16:19
par adrien17 » 31 Jan 2015, 16:19
Carpate a écrit:Pour faire apparaître le 1, il faut faire apparaître le dénominateur :
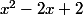
dans l'expression du dénominateur :

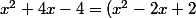 +6x -6=(x^2-2x+2) +6(x -1))
Au risque de paraître bête, je ne comprend pas "il faut faire apparaître le dénominateur dans l'expréssion du dénominateur"... N'est-ce pas plutôt dans l'expression du "numérateur" ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 31 Jan 2015, 16:27
par Carpate » 31 Jan 2015, 16:27
adrien17 a écrit:Au risque de paraître bête, je ne comprend pas "il faut faire apparaître le dénominateur dans l'expréssion du dénominateur"... N'est-ce pas plutôt dans l'expression du "numérateur" ?
Le numérateur :

le dénominateur :
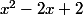
Pour faire apparaître
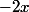
dans

on soustrait
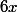
Pour faire apparaître
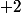
dans

on ajoute

 = x^2-2x+4)
-
adrien17
- Messages: 5
- Enregistré le: 11 Jan 2015, 13:56
-
 par adrien17 » 31 Jan 2015, 16:32
par adrien17 » 31 Jan 2015, 16:32
Carpate a écrit:Le numérateur :

le dénominateur :
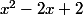
Pour faire apparaître
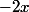
dans

on soustrait
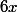
Pour faire apparaître
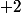
dans

on ajoute

 = x^2-2x+6)
D'accord merci, je vais essayer de terminer mon exo !
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 31 Jan 2015, 16:55
par annick » 31 Jan 2015, 16:55
Bonjour,
je ne comprends pas où est la difficulté du 2) (à part erreur d'étourderie).
On cherche :
f(x) -1 = (x² + 4x - 4)/(x² -2x +2) -1
=[ x²+4x-4 -(x²-2x+2)]/(x²-2x+2) (en mettant tout au même dénominateur)
=(x²+4x-4-x²+2x-2)/(x²-2x+2)
=(6x-6)/(x²-2x+2)
=6(x-1)/(x²-2x+2) qui est bien le résultat cherché.
-
adrien17
- Messages: 5
- Enregistré le: 11 Jan 2015, 13:56
-
 par adrien17 » 31 Jan 2015, 17:35
par adrien17 » 31 Jan 2015, 17:35
annick a écrit:Bonjour,
je ne comprends pas où est la difficulté du 2) (à part erreur d'étourderie).
On cherche :
f(x) -1 = (x² + 4x - 4)/(x² -2x +2) -1
=[ x²+4x-4 -(x²-2x+2)]/(x²-2x+2) (en mettant tout au même dénominateur)
=(x²+4x-4-x²+2x-2)/(x²-2x+2)
=(6x-6)/(x²-2x+2)
=6(x-1)/(x²-2x+2) qui est bien le résultat cherché.
En lisant cette réponse, je me suis rendu compte que je restais bloqué à cause d'une stupide erreur de signe... :mur:
Merci de votre aide !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
