SEVs L1

[JasonG]

Bonjour,
Voici l'énoncé:

Dans R^4, notons F le sous-espace vectoriel engendrée par les vecteurs suivants:
u = (1, 1, 2, 3) v = (;)2, 1, 3, 2) w = (1, 2, 3, 7)
Déterminer un système d’équations linéaires S dont l’ensemble des solutions soit le sous-espace vectoriel F.

J'ai répondu ainsi:
J'ai posé la matrice ajoutée suivante:


et j'ai obtenu:


Donc est-ce que l'ensemble des solutions de

constitue le sous espace vectoriel engendrée F?

[hari05]

Bonjour,
Voici l'énoncé:

Dans R^4, notons F le sous-espace vectoriel engendrée par les vecteurs suivants:
u = (1, 1, 2, 3) v = (;)2, 1, 3, 2) w = (1, 2, 3, 7)
Déterminer un système d’équations linéaires S dont l’ensemble des solutions soit le sous-espace vectoriel F.

J'ai répondu ainsi:
J'ai posé la matrice ajoutée suivante:


et j'ai obtenu:


Donc est-ce que les solutions de

sont le sous espace vectoriel engendrée F?

Bonjours

tu peux me dire comment postuler un execice stp

[Luc6]

ça ne serait pas tout simplement:

;)1(u) + ;)2(v) +;)3(w) ???

[JasonG]

Il faut que ce soit un système d'équations au final. Le système marche bien pour les 3 vecteurs. Je supposais que du coup ça marchait aussi avec toute combinaison linéaire de ces 3 vecteurs. Mais je ne suis pas sur. Je ne suis même pas sur de mon raisonnement depuis le début. Personne semble pouvoir aider :triste:

[JasonG]

ok, je viens de trouver une erreur. Je corrige

[paquito]

si on appelle A ta première matrice, en remplaçantpar 1 on obtient un déterminant non nul donc u, v et w sont linéairement indépendant et engendrent donc un hyperplan de d'équation :;

tu trouve cette équation en écrivant que dét(A)=0 , mais il faut faire le calcul à la main et il n'y a pas beaucoup de simplification possible; il faut s'appliquer!

[JasonG]

mais si je remplace x1, x2, x3, x4, par 1, 1, 1, 1, lorsque je calcule le déterminant, je n'obtiendrait qu'une valeur numérique, non?

[paquito]

Oui, mais ça prouve que tes 4 vecteurs sont linéairement indépendants donc a fortiori u, v et w aussi, sinon le déterminant serait nul car si w=au+bv, avec a²+b² non nul et en posant t=(1, 1, 1, 1), tu aurais:

dét(u, v, w, t)=dét( u, v, au+bv, t)=dét(u, v,au, t)+dét(u, v, bv, t)=0+0 (2 colonnes proportionnelles);

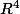
c'est donc un moyen rapide (calculatrice) pour savoir que u, v et w vont engendrer un s.e.v. de dimension 3 qui est l'ensemble des vecteurs ; cest donc un hyperplan de qui aura pour équation dét(A)=0 avec comme 4° colonne ; évidemment c'est un calcul qu'il faut faire à la main et qui est un peu pénible.

En développant ce déterminant suivant la dernière colonne pour calculer les cofacteurs à la calculatrice, j'obtiens comme équation de ; j'ai vérifié.

[JasonG]

Super, merci beaucoup.
Juste une autre question. Comment peut-on savoir à priori que le vecteur t(1,1,1,1) est linéairement indépendant de u, v et w? Comment l'as tu choisi?

[paquito]

Super, merci beaucoup.
Juste une autre question. Comment peut-on savoir à priori que le vecteur t(1,1,1,1) est linéairement indépendant de u, v et w? Comment l'as tu choisi?

Un peu au hasard, si j'avais trouvé det(A)=0 j'aurais regardé si u, v et w étaient linéairement dépendant, ce qui aurait un peu compliqué les choses car F serait de dimension 2;
c'est un bricolage permis par la calculatrice, sinon on regarde les déterminants d'ordre 3 issus de u,v et w et en fait ça va aussi vite.

[chan79]

salut
On peut remarquer que F est engendré par u et v puisque w=3u+v

(x,y,z,t) appartient à F ssi il existe (a,b) tel que :

x=a-2b
y=-a+b
z=2a-3b
t=-3a+2b
ces égalités impliquent que x-y=z et x+4y=t

F est l'ensemble des (x,y,z,t) tels que


Par exemple, avec x=3 et y =1 on a (x,y,z,t)=(3,1,2,7)
on calcule a et b vérifiant
3=a-2b
1=-a+b
on trouve a=-5 et b=-4

et on vérifie que (3,1,2,7)=-5u-4v

[JasonG]

salut
On peut remarquer que F est engendré par u et v puisque w=3u+v

Il se peut que ça marche pas avec la dernière ligne (au signe près), puisqu'on à 3x(-3)+2=-7. :triste:

[chan79]

Il se peut que ça marche pas avec la dernière ligne (au signe près), puisqu'on à 3x(-3)+2=-7. :triste:

on a bien

3 (1, 1, 2, 3) + (;)2, 1, 3, 2) = (1, 2, 3, 7)

tu as bien mis -7 dans l'énoncé

[JasonG]

on a bien

3 (1, 1, 2, 3) + (;)2, 1, 3, 2) = (1, 2, 3, 7)

tu as bien mis -7 dans l'énoncé

Oui, désolé, je me suis trompé ensuite en écrivant 7 dans la matrice.

Merci beaucoup pour votre aide, c'est très apprécié

[paquito]

Evidemment avec -7, ça change tout puisque les 4 déterminants d'ordre 3 sont nuls donc f est de dimension 2 (la dimension 1 étant trivialement excluse). Chan t'a montré comment arriver à exprimer f comme l'intersection de 2 hyperplans. Comme ça, finalement tu auras vu 2 situations!