Étude de fonction

[Lili4550]

Bonjour,

J'aurai aimé savoir si quelqu'un avez la correction du 2ème exercice du sujet présent dans le lien suivant. Sinon est ce que quelqu'un pourriez m'aider à comprendre ce qu'il faut faire? J'aimerai m'entraîner.

D'avance je vous remercie.

http://www.concours.developpement-durable.gouv.fr/IMG/pdf/ITPE-I-2010-Mathematiques_composition_1_cle0a18c8-1.pdf

[fatal_error]

hello,

qu'as-tu fait et qu'est-ce que tu comprends pas?
énoncé exo2:

[Lili4550]

voici ce que j'ai fait. Cependant je n'ai pas beaucoup avancer car j'ai du mal à comprendre ce qu'est f(x).
Merci beaucoup pour votre aide.

on désigne par f une fonction dérivable d'une variable réelle vérifiant pour tout couple (x,y) de nombre réels, la relation f(x+y)=(f(x)+f(y))/(1+f(x)f(y)) (*)
L'objectif de cet exercice est de trouver les fonctions f vérifiant la relation (*)

1)montrer que pour tout réel t, on a: -1<(ou égale) 2t/1+t^2 <(ou égale à 1

Ce que j'ai fait:
Pour cette question j'ai résolu l'inéquation -1<(ou égale) 2t/(1+t^2) et j'ai obtenu comme racine -1 puis j'ai résolu l'inéquation 2t/(1+t^2) < (ou égale) 1et j'ai obtenu comme racine 1

2) en déduire que pour tout réel x, on a -1<(ou égale ) f(x) <1


Pour cette question je ne vois pas j'ai du mal car il y a deux variable x et y et du coup je bloque pour la suite

3) trouver toutes les fonctions f constantes vérifiant la relation (*)

4) désormais jusqu'à la fin de l'exercice, on suppose f non constante
A) peut il exister un réel x0 de sorte que l'on ait, ou bien f(x0)=1 ou bien f(xo)=-1? Autrement dit a-t-on quelque soit x qui appartient à R, -1 B) calculer f(0) et en déduire que f est fonction impaire

Ce que j'ai fait:
f(0) donc x+y=0 d'où f(0)=0

f impaire ssi f(-x)=-f(x)

Donc f(-x+y)=(f(-x) + f(y))/(1+f(-x)f(y))= -f(x+y)


5) on pose f'(0)=a. En utilisant la définition de la dérivée, montrer que
Quelque soit x qui appartient à R, f'(x)=a(1-(f(x)^2)


6) en déduire les variations de f selon le signe de a

Ce que j'ai fait:
Je pose f(x)=x

Quelque soit a>0. 1-x^2>0
Racine évidente x1=-1 et x2=1

S1=]-1,1[ f est strictement croissante sur l'intervalle ]-1,1[


Quelque soit a<0 1-x^2<0
Racine évidente x1=-1 et x2=1

S2=]- infini; -1[ U ]1;+ infini[. f est strictement décroissante sur l'intervalle S2


7) on pose l= lim (x-> infini) de f(x). Justifier l'existence de cette limite.

lim (x-> - infini) f(x)= - infin lim (x-> + infini) f(x)= + infini

8) calculer f(2^(n+1)) en fonction de f(2^n) et déterminer les valeurs possible de I

9) montrer que f réalise une bijection de R -> ]-1,1[

Ce que j'ai fait:
f est une fonction strictement croissante sur I= ]-1,1[. f est défini et continue sur cet intervalle.
Elle réalise une bijection de I sur ]-infini ; + infini[

10) justifier que f^-1 est dérivable et calculer (f^-1)' en fonction de a

Ce que j'ai fait:
La fonction f^-1 est définie et a valeur dans I, strictement croissante sur R donc f est dérivable sur R.


11) justifier que f^-1(0)=0 et expliciter f^-1(y) pour tout y appartenant ]-1,1[

12) en déduire enfin toutes les fonctions f, non constantes et dérivables vérifiant (*)

[fatal_error]

pour 2)
t'as qu'a prendre x'= 1/2x, et y'=1/2x
du coup tu peux poser t = f(x')
et tu as
f(x) = f(x'+y') = (t+t)/(1+t^2)

[Lili4550]

Ah oui merci beaucoup du coup ça devrait aussi me débloque pour la suite comme j'ai f(x)

[capitaine nuggets]

Ah oui merci beaucoup du coup ça devrait aussi me débloque pour la suite comme j'ai f(x)

Une petite constatation (on ne sait jamais, ça peut servir) : la fonction "tangente hyperbolique" est une solution particulière :+++:

[capitaine nuggets]

Salut !

3) trouver toutes les fonctions f constantes vérifiant la relation (*)

En posant, pour tout , , où désigne une constante réelle, cela revient à résoudre l'équation d'inconnue , :++:

4) désormais jusqu'à la fin de l'exercice, on suppose f non constante
B) calculer f(0) et en déduire que f est fonction impaire

Là ce n'est pas évident à priori. D'après l'égalité que vérifie , pour 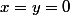, on a :

[CENTER][/CENTER]

En posant , trouver revient à résoudre l'équation d'inconnue , .

f impaire ssi f(-x)=-f(x)

Part de l'égalité (*) en remplaçant par et par :+++:

[zaidoun]

Pour 5) soit , on a

Remplacer f(x+t) par la relation (*), tu trouves que
d'où le résultat.