Série exponentielle

[ludelu95170]

Bonjour Je suis nouveau, c'est mon premier message
J'ai un devoir où il y aune question où j'ai du mal
La voici :
En utilise l'écriture e^1 = exp(-1) et la série exponentielle
Démontrer :


Je vous remercie pour votre aide et bonne fête à tous
Ludelu

[eriadrim]

Salut,

Si tu utilise la serie exponentielle tu devrais obtenir une série dont le premier terme est

Tu as plus qu'a utiliser une conséquence du théorème spécial qui dit que si une serie vérifie les conditions du théorème spécial à partir du premier terme, alors la somme est plus petite en valeur absolue au premier terme et est du signe du premier terme

[zaidoun]

La série est alternée et convergente, et on a


où a_N est le terme général de la série (a_N= (-1)^N /N!)

utiliser cette propriété pour trouver le résultat.

[ludelu95170]

La série est alternée et convergente, et on a


où a_N est le terme général de la série (a_N= (-1)^N /N!)

utiliser cette propriété pour trouver le résultat.

Je suis désolé mais je n'ai pas compris.
Je sais que . On veint juste de commencer les série donc je n'ai pas beaucoup de maîtrise de cette notion.

Que signifie ?

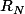
[zaidoun]

mais tu as e^{-1}, à quoi égale e^{-1}=?

R_N est le reste d'ordre N.
Tu connais les séries alternées?

[ludelu95170]

mais tu as e^{-1}, à quoi égale e^{-1}=?

R_N est le reste d'ordre N.
Tu connais les séries alternées?

Je sais que alterné cela signifie que ça change de signe
Sinon et ensuite j'utilise au dénominateur la formule de la série exponentielle avec u = 1 , est ce que c'est ça ?

[zaidoun]

utilises directement la formule avec u=-1

[ludelu95170]

utilises directement la formule avec u=-1

J'obtiens donc :

Ensuite comment j’introduis l'encadrement.

[zaidoun]

J'obtiens donc :

Ensuite comment j’introduis l'encadrement.

Comme je t'ai dit ,utilises la propriété du reste R_N (avec valeur absolue, j'ai corrigé ça) pour trouver la deuxième inégalité.

[ludelu95170]

Comme je t'ai dit ,utilises la propriété du reste R_N (avec valeur absolue, j'ai corrigé ça) pour trouver la deuxième inégalité.

J'ai regardé et j'ai lu :

Donc si j'applique ceci j'obtiens : car le premier terme de la somme est 1

[zaidoun]

J'ai regardé et j'ai lu :

Donc si j'applique ceci j'obtiens : car le premier terme de la somme est 1

mais il faut l’utiliser pour le reste d'ordre 2p+1 càd | R_{2p+1} |<= | a_{2p+2} |, tu trouves exactement la deuxième inégalité.

[ludelu95170]

mais il faut l’utiliser pour le reste d'ordre 2p+1 càd | R_{2p+1} |<= | a_{2p+2} |, tu trouves exactement la deuxième inégalité.

ah d'accord. Un grand merci.
Si j'ai bien compris je coupe la somme en deux :
et on a

[paquito]

Une propriété simple des séries alternées convergentes est que le reste de rang n est majoré par la valeur absolue du premier terme négligé. Application immédiate ici!