Salut,
Déjà, je pense que ça serait plus simple d'écrire que
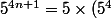^n)
et de calculer une bonne fois pour toute combien vaut

modulo 13.
Ensuite, effectivement, le -1 de 4n-1 peut donner l'impression de poser problème.
A ton niveau, je vois (au moins) deux solutions :
1) Soit tu "pose" m=n-1 de façon à ce que 4n-1=4m+3 et cette fois 3 est positif (bien sûr il faut faire la même chose avec l'autre exposant en écrivant que 4n+1=4m+5. Et ne pas oublier non plus que, vu que l'énoncé était (sans doute...) "Montrer que pour tout n>=1 on a..." il faut remplacer par "Montrer que pour tout m>=0 on a..."
2) Soit tu dit que, vu que 18 est premier avec 13, le nombre

est divisible par 13 si et seulement si

est divisible par 13 et, comme
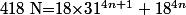
, ça te "vire" le -1 qui t'emmerdais.
P.S. Concernant la première méthode, tu n'est même pas obligé de "poser" quoi que ce soit : tu paut tout aussi bien écrire directement que
^{n-1})
ce qui revient exactement au même et évite d'introduire une "lettre" en plus.