Résolution Équation parti entière

[Altaiir8]

Bonsoir,

Comment puis je résoudre une équation tel que [2x-1] = [x-4] ?

J'ai bien essayer de la faire en posons [x] = k mais je ne trouve que -3 comme solution hors dans la correction il y'a mit :



Apres le -3 que j'ai trouvé je n'ai vraiment rien compris ... surtout pourquoi utiliser k + 1/2 ?!

Merci d'avance

[mathelot]

bonjour,

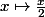
[chan79]

Bonsoir,
surtout pourquoi utiliser k + 1/2 ?!

Merci d'avance

c'est pour encadrer 2x par deux entiers consécutifs (dans les deux cas envisagés).

Sinon, c'est pas mieux mais on pourrait chercher quels sont les entiers k qui pourraient vérifier les inégalités:
k-9
et
2k+7<k+1 donc k<-6
Les seules valeurs de k strictement comprises entre -9 et -6 sont -7 et -8
Premier cas (k=-8)
il faut résoudre le système:
-8<=2x-1<-7
-8<=x-4<-7
on obtient
-3,5<=x<-3
-4<=x<-3
ce qui donne S1= [-3,5;-3[
Second cas (k=-7)
-7<=2x-1<-6
-7<=x-4<-6
cela donne S2=[-3;-2,5[


On réunit S1 et S2 et on trouve le même résultat.

[Altaiir8]

c'est pour encadrer 2x par deux entiers consécutifs (dans les deux cas envisagés).

Sinon, c'est pas mieux mais on pourrait chercher quels sont les entiers k qui pourraient vérifier les inégalités:
k-9
et
2k+7<k+1 donc k<-6
Les seules valeurs de k strictement comprises entre -9 et -6 sont -7 et -8
Premier cas (k=-8)
il faut résoudre le système:
-8<=2x-1<-7
-8<=x-4<-7
on obtient
-3,5<=x<-3
-4<=x<-3
ce qui donne S1= [-3,5;-3[
Second cas (k=-7)
-7<=2x-1<-6
-7<=x-4<-6
cela donne S2=[-3;-2,5[


On réunit S1 et S2 et on trouve le même résultat.

Ok merci j'ai compris avec ta solution, c'est tout de suite plus simple !

[zygomatique]

salut

si l'on sait que E(x + k) = E(x) + k pour tout entier k

alors l'équation devient E(2x) - 1 = E(x) - 4 <=> E(2x) = E(x) - 3

si E(x) = k =< x < k + 1/2 alors E(2x) = 2k soit 2k = k - 3 <=> k = -3 et x est dans [-3; -2,5[

si E(x) = k et k + 1/2 =< x < k + 1 alors E(2x) = 2k + 1 soit 2k + 1 = k - 3 donc k = -4 et x est dans [-3,5 ; - 3[

....

[Altaiir8]

salut

si l'on sait que E(x + k) = E(x) + k pour tout entier k

alors l'équation devient E(2x) - 1 = E(x) - 4 E(2x) = E(x) - 3

si E(x) = k = k = -3 et x est dans [-3; -2,5[

si E(x) = k et k + 1/2 =< x < k + 1 alors E(2x) = 2k + 1 soit 2k + 1 = k - 3 donc k = -4 et x est dans [-3,5 ; - 3[

....

Merci pour ta réponse Zygomatique mais je dois avouer que j'ai toujours un problème avec le k +1/2 :s

[Ben314]

Salut,
L'astuce (si on peu dire), c'est que, si E(x)=k, ça signifie que k<=xC'est pour ça qu'on considère les deux cas en question.

[Altaiir8]

Salut,
L'astuce (si on peu dire), c'est que, si E(x)=k, ça signifie que k<=x<k+1 donc 2k<=2x<2k+2 ce qui signifie qu'il y a deux possibilités pour E(2x) : soit 2k, soit 2k+1 selon que 2x est dans [2k,2k+1[ ou bien dans [2k+1,2k+2[, c'est à dire selon que x est dans [k,k+1/2[ ou bien dans [k+1/2,k+1[.
C'est pour ça qu'on considère les deux cas en question.

Ah ok merci, je comprend un peu mieux maintenant le k+1/2 ^^

[zygomatique]

ou encore la multiplication par 2 dilate un segment de longueur 1 en un segment de longueur 2 .... qui peut donc contenir plus d'un entier .... ce qui pose problème quand on veut prendre la partie entière....