Polynôme - Equation
14 messages
- Page 1 sur 1
Polynôme - Equation
Voilà j'ai l'équation suivante :
(E): 6x4 + 5x3 - 38x2 + 5x + 6 = 0 (les chiffres après x sont les exposants.
Et voilà la question :
Montrer que si x est solution de l'équation (E) alors x est la solution de deux équations de second degré (E'1) et (E'2) que l'on déterminera.
Vous pouvez pas m'expliquer svp ??!
(E): 6x4 + 5x3 - 38x2 + 5x + 6 = 0 (les chiffres après x sont les exposants.
Et voilà la question :
Montrer que si x est solution de l'équation (E) alors x est la solution de deux équations de second degré (E'1) et (E'2) que l'on déterminera.
Vous pouvez pas m'expliquer svp ??!
Un polynôme du quatrième dégré a obligatoirement quatre solutions (réelles ou complexes). E peut donc se factoriser sous la forme :
6(x-x1)(x-x2)(x-x3)(x-x4).
En groupant les facteurs par deux on obtient deux équations du second dégré E1 et E2 (Il y a plusieurs possibilités). Autrement dit, si E1 = (x-x1)(x-x2) alors x1 qui est solution de E1 est également solution de E car E= E1*E2 (Si E1 = 0 ==> E =0)
Factorisons E
On essaye les diviseurs du terme indépendant : 6
Ce sont -6, -3, -2, -1 1, 2, 3, 6
On trouve facilement que E(-3)= 0 et E(2) = 0 (C'est à dire que l'on remplace x par -3 et puis par 2 et on trouve E=0)
Donc E est divisible par x+3 et x-2
On obtient : E=(x-2)(6x3+17x2-4x-3)=(x-2)(x+3)(6x2-x-1)
Le dernier facteur se factorise aussi facilement
Finalement :
E=6(x-2)(x+3)(x+1/3)(x-1/2)
Tu groupes les facteurs par deux pour obtenir E1 et E2
Par exemple :
E=(x2-x-6)(6x2-x-1)
Jacques
6(x-x1)(x-x2)(x-x3)(x-x4).
En groupant les facteurs par deux on obtient deux équations du second dégré E1 et E2 (Il y a plusieurs possibilités). Autrement dit, si E1 = (x-x1)(x-x2) alors x1 qui est solution de E1 est également solution de E car E= E1*E2 (Si E1 = 0 ==> E =0)
Factorisons E
On essaye les diviseurs du terme indépendant : 6
Ce sont -6, -3, -2, -1 1, 2, 3, 6
On trouve facilement que E(-3)= 0 et E(2) = 0 (C'est à dire que l'on remplace x par -3 et puis par 2 et on trouve E=0)
Donc E est divisible par x+3 et x-2
On obtient : E=(x-2)(6x3+17x2-4x-3)=(x-2)(x+3)(6x2-x-1)
Le dernier facteur se factorise aussi facilement
Finalement :
E=6(x-2)(x+3)(x+1/3)(x-1/2)
Tu groupes les facteurs par deux pour obtenir E1 et E2
Par exemple :
E=(x2-x-6)(6x2-x-1)
Jacques
axylin12 a écrit:En fait j'aimerais beaucoup que quelqu'un me fasse la question car je pourrais ainsi accéder aux réponses, à la compréhension mais également à la rédaction (comment rédiger la réponse à ce genre de question) !
Pour que tu puisses avancer je crois qu'il vaut mieux que tu nous donnes ta version après avoir compris ce que mon camarade a expliqué. Si t'as pas compris un étape tu demandes!
On peut rédiger pour toi mais ca va te servir à rien ( je pense)
C'est vrai que ce que t'as proposé comme Solution Jaques n'est pas évident ( trouver deux racines évidentes)
On fait, ce que t'as di au début pour etre exploiter ainsi:
6x4 + 5x3 - 38x2 + 5x + 6 =6(x²+ax+b)(x²+cx+d) ( avec a, b, c et d rèels)
( ca c'est toujours vrai si je me trompe pas)
et là t'auras un système de 4 équations à 4 inconnus mais facile ( en effet, le système contient des équations en deux inconnus seulement). Le reste n'est qu'un calcul et ça doit etre clair ca sinon...
On fait, ce que t'as di au début pour etre exploiter ainsi:
6x4 + 5x3 - 38x2 + 5x + 6 =6(x²+ax+b)(x²+cx+d) ( avec a, b, c et d rèels)
( ca c'est toujours vrai si je me trompe pas)
et là t'auras un système de 4 équations à 4 inconnus mais facile ( en effet, le système contient des équations en deux inconnus seulement). Le reste n'est qu'un calcul et ça doit etre clair ca sinon...
Bonsoir !
Est-ce que tu as recopié l'énoncé exact ? Parce que tu dis :
or si on factorise le polynôme de degré 4 en un produit de deux polynômes de degré 2, x solution de E implique que x est solution d'une des deux équations du second degré obtenues ainsi.
Est-ce que tu as recopié l'énoncé exact ? Parce que tu dis :
axylin12 a écrit:Montrer que si x est solution de l'équation (E) alors x est la solution de deux équations de second degré (E'1) et (E'2) que l'on déterminera.
or si on factorise le polynôme de degré 4 en un produit de deux polynômes de degré 2, x solution de E implique que x est solution d'une des deux équations du second degré obtenues ainsi.
abcd22 a écrit:Bonsoir !
Est-ce que tu as recopié l'énoncé exact ? Parce que tu dis :
or si on factorise le polynôme de degré 4 en un produit de deux polynômes de degré 2, x solution de E implique que x est solution d'une des deux équations du second degré obtenues ainsi.
l'énoncé me semble acceptable dans la mesure ou x est une inconnue.
Ya juste un petit détail. Il fallait dire "x est une solution" et pas "x est la solution" car meme dans le cas d'une polynôme de degrés deux on peut pas parler de la solution ( sauf dans le que particulier ou delta =0 bien sûr)
Cherche pas loin le but de l'exo est de saoir décomposer les polynômes sur R ni + ni -.
Coridalement,
Je vois pas trop l'intérêt de la question, autant dire qu'on veut une décomposition du polynôme tout de suite, puisqu'on n'a pas plus de méthode générale pour trouver deux facteurs de degré 2 que pour trouver les 4 racines (en écrivant 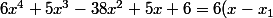(x-x_2)(x-x_3)(x-x_4)) on a 4 inconnues à trouver, soit autant que pour trouver les facteurs de degré 2), et en plus pour les facteurs de degré 2 il y a plusieurs possibilités... Enfin bref on retiendra que l'énoncé n'est pas très clair.
on a 4 inconnues à trouver, soit autant que pour trouver les facteurs de degré 2), et en plus pour les facteurs de degré 2 il y a plusieurs possibilités... Enfin bref on retiendra que l'énoncé n'est pas très clair.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 150 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
