Nombre de roues

[alitshe]

Bonjour, je suis en préparation CAPES et pour reprendre doucement l'année nous devont résoudre le problème suivant de deux manières différentes mais ... je n'y arrive pas !
Voici le problème : Dans une cour d'école on aperçoit des tricycles (3roues) et des petites voitures (4 roues). On dénombre 80 roues. Combien y a t-il de tricycles et de petites voitures ??

j'ai essayé de résoudre ce problème comme une équation du type 80=3t+4v
mais je n'y arrive pas

[zygomatique]

salut

3et 4 sont premiers entre eux donc il existe u et v tels que 4u + 3v = 1

u = 1 + 3k et v = -1 - 3k ...



autre méthode ::

80 - 4v est multiple de 4 donc t = 4s

80 = 12s + 4v <=> 20 = 3s + v

s = 6 et v = 2 est solution ...

20 = 3s + v
20 = 3.6 + 2

par soustraction :: 3(s - 6) = 2 - v

...

[alitshe]

merci mais avec ça je pense que je vais répondre 20 voitures car 4*20=80 ... car je ne comprends pas

[beagle]

la deuxième soluce de zygomatique doit passer facilement.
80= 3t+4v
il faut bien que t soit un multiple de 4,
alors tu l'appelles 4x(quelque chose), zygo l'a appelé 4x s

alors
80 = 3x4xs + 4 v
20= 3s + v

et là tu déroules les possibles
s= 1, alors v=17
s=2, alors v= 14
s=3, v= 11
...autre soluces

lorsque s= 1, cela signifie qu'il y a 4s tricycles, donc 4 tricyles et 17 voitures
alors 3x4 + 4x17 = 80 roues

lorsque s=2, il y a 4x2= 8 tricycles
3x8 + 4x14 roues

[alitshe]

Haaa oui j'ai pigé merci ! j'étais pas sur ce genre de solution j'ai essayé de résoudre une équation diophantienne et je n'ai jamais compris la résolution de ce type d'équation vu que je viens encore de rater je n'ai trouvé aucun solution :(
mais effectivement cette méthode est simple et efficace ! :)

[alitshe]

en fait j'ai pas compris pour ce t dois être un multiple de 4... je n'en peut plus ca devrait être un exo simple!!!

[alitshe]

j'ai compris !!! :)

[zygomatique]

j'ai compris !!!

80 = 4v + 3t 4(20 - v) = 3t

4(20 - v) est multiple de 4 donc 3t aussi

or 4 ne divise pas 3 donc divise t

donc t = 4s

donc 20 - v = 3s

v + 3s = 20

s = 0 => v = 20
s = 1 => v = 17
s = 2 => v = 14


et plus généralement

4(20 - v) = 3t

20 - v = 3k
t = 4k



v = 20 - 3k
t = 4k

....

[wserdx]

Je propose une petite astuce (juste une approche légèrement différente) qui peut éventuellement resservir.
L'équation "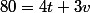" est de type "affine" même si on ne cherche que les solutions entières. On peut exprimer toute solution du problème comme somme d'une solution particulière et d'une solution sans second membre "".
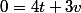Une solution particulière est par exemple
Les solutions (entières) de l'équation sans second membre s'obtiennent facilement comme
pour k entier quelconque.
Les solutions générales sont donc
Comme de plus j'imagine qu'on impose et , on déduit une contrainte supplémentaire sur :
soit Ce qui donne au final 7 solutions.

[chan79]

salut
4v+3t=80 équivaut à v=20- (3t)/4
t est donc nécessairement multiple de 4; c'est facile de lister:
(t,v)) prend les valeurs (0,20), (4,17), (8,14), (12,11), (16,8), (20,5), (24,2)
Comme "on aperçoit des tricycles", on enlève la première solution et il en reste 6

[beagle]

très intéressant, merci wserdx.(et zygomatique, chan79 )

Comme j'ai bossé cet été y=ax+b pour ma fille, je m'étais posé justement la question,à savoir
si on ne pouvait pas s'en servir dans le cas présent qui ressemble bien que différent,...
ben voilà la réponse!

[wserdx]

Comme "on aperçoit des tricycles", on enlève la première solution et il en reste 6

argh, bien vu...
Comme quoi, la contrainte ce n'est même pas et
mais et , "des" est pluriel!

[beagle]

wserdx:"L'équation "" est de type "affine" même si on ne cherche que les solutions entières"

Nos amis mathématiciens se contenteront de lire les équations formulées par zygomatique, chan79 et wserdx,
pour les collégiens comme moi, on peut les rassurer, les assurer en posant sur un graphe
les solutions avec les points de coordonnées:
(4,17) , (8,14), (12,11), (16,8)
quand on décale x de 4, on décale y de 3, c'est la pente de la droite,le a de y= ax+b
et la soluce (0,20) qui est un point de la droite est le point (0,b) de y=ax+b
donc un point et une pente c'est ce qui convient à un collégien.
Ben j'aime bien voir, regarder, c'est pas que je vous crois pas les gars,...

(peut-ètre qu'alitshe sera intéressé de consolider ça comme moi, ce que raconte l'équation algébrique peut se voir et s'associer au visuel-graphe-géométrie)

[wserdx]

Bonjour, je suis en préparation CAPES

(peut-ètre qu'alitshe sera intéressé de consolider ça comme moi, ce que raconte l'équation algébrique peut se voir et s'associer au visuel-graphe-géométrie)

Je n'en doute pas... même si je n'ai aucune idée du niveau exigé d'un candidat au CAPES :lol3:
Quant aux collégiens, j'ai une fille qui rentre en cinquième, mais je ne suis pas non plus très attentif au contenu de son programme ni aux méthodes pédagogiques qu'elle va rencontrer... :hein:
(je ne suis pas, vous l'aurez compris, un vieux routier de l'enseignement, j'espère donc que ma proposition d'approche du problème n'aura froissé personne...)

[zygomatique]

Je propose une petite astuce (juste une approche légèrement différente) qui peut éventuellement resservir.
L'équation "" est de type "affine" même si on ne cherche que les solutions entières. On peut exprimer toute solution du problème comme somme d'une solution particulière et d'une solution sans second membre "".
Une solution particulière est par exemple
Les solutions (entières) de l'équation sans second membre s'obtiennent facilement comme
pour k entier quelconque.
Les solutions générales sont donc
Comme de plus j'imagine qu'on impose et , on déduit une contrainte supplémentaire sur :
soit Ce qui donne au final 7 solutions.

ce n'est pas une approche différente, c'est une vision globale et générale d'un cas particulier !!!

tout espace affine est la somme d'un espace vectoriel (tangent) et d'un point appartenant à cet espace affine

évidemment le point particulier (0, 20) est immédiat (qui à nouveau est un cas particulier en dimension n lorsqu'on annule toutes les coordonnées sauf une)

on a la même situation dans les équations différentielles avec second membres (somme des solutions de l'équation homogène (l'espace vectoriel tangent) et d'une solution particulière

les suites récurrentes (somme d'une solution particulière et de s solutions de l'équation homogène)

....

à noter que dans le cas des équations diophantiennes la difficulté réside dans le fait qu'on veut des solutions entières ...

:lol3: