Il y a des erreurs ??
22 messages
- Page 1 sur 2 - 1, 2
il y a des erreurs ??
voila je voulais savoir si il y avait des erreurs?
l'enonce
exercice 1 :
soit P(x) un polynome du second degré qui admet 2 racines dinstinctes : x1 et x2
p(x) = ax²+bx+c
1) demontrer que la somme S des racines est egale à x1 +x2 = -b/a et que leur produit P est egal
à x1x2 = c/a
2) demontrer alors que x1 et x2 sont solutions de l'equation : ax² - S x + P = 0
3) application ; trouver 2 nombres connaissant leur somme 18 et leur produit 72
reponse
1)... je suis arrivé a
p(x)=a(x²-Sx+P)
dois je developer avec a... >> ax²-aSx+aP ??
2)x1 et x2 sont donc les solutions de l'equation ax²-Sx+P=0 mais comme a est different de zero cette equation equivaut a l'equation x2-Sx+P=0
phrase correcte pour laquestion??
3) donc on a
x²-18x+72
delta=324-288=36
racine de 36=6
x1=12 et x2=6
donc s= 12 et 6
je dois rediger comme ca ou je dois mettre des phrases??
l'enonce
exercice 1 :
soit P(x) un polynome du second degré qui admet 2 racines dinstinctes : x1 et x2
p(x) = ax²+bx+c
1) demontrer que la somme S des racines est egale à x1 +x2 = -b/a et que leur produit P est egal
à x1x2 = c/a
2) demontrer alors que x1 et x2 sont solutions de l'equation : ax² - S x + P = 0
3) application ; trouver 2 nombres connaissant leur somme 18 et leur produit 72
reponse
1)... je suis arrivé a
p(x)=a(x²-Sx+P)
dois je developer avec a... >> ax²-aSx+aP ??
2)x1 et x2 sont donc les solutions de l'equation ax²-Sx+P=0 mais comme a est different de zero cette equation equivaut a l'equation x2-Sx+P=0
phrase correcte pour laquestion??
3) donc on a
x²-18x+72
delta=324-288=36
racine de 36=6
x1=12 et x2=6
donc s= 12 et 6
je dois rediger comme ca ou je dois mettre des phrases??
Salut,
comme x1et x2 sont racines du polynôme p(x)=ax²+bx+c alors p(x)=a(x-x1)(x-x2)
avec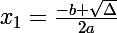 et
et 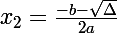
donc
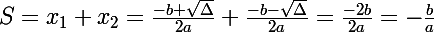
essaies le produit P
il vaut mieux mettre des phrases pour introduire ta demonstration
soit P(x) un polynome du second degré qui admet 2 racines dinstinctes : x1 et x2
p(x) = ax²+bx+c
1) demontrer que la somme S des racines est egale à x1 +x2 = -b/a et que leur produit P est egal
à x1x2 = c/a
comme x1et x2 sont racines du polynôme p(x)=ax²+bx+c alors p(x)=a(x-x1)(x-x2)
avec
donc
essaies le produit P
je dois rediger comme ca ou je dois mettre des phrases??
il vaut mieux mettre des phrases pour introduire ta demonstration
barbot a écrit:1)... je suis arrivé a
p(x)=a(x²-Sx+P)
Tout seul ? Bravo !
Voir aussi...http://www.maths-forum.com/showthread.php?t=18508
J'appelle ça du multipost !
Quidam a écrit:Tout seul ? Bravo !
Voir aussi...http://www.maths-forum.com/showthread.php?t=18508
J'appelle ça du multipost !
non c'est grace a toi mais ma prof aime qu'on redige bien donc je voulais savoir si fallait mettre des phrases ...
fonfon a écrit:Salut,
comme x1et x2 sont racines du polynôme p(x)=ax²+bx+c alors p(x)=a(x-x1)(x-x2)
avecet
donc
essaies le produit P
il vaut mieux mettre des phrases pour introduire ta demonstration
mais ca c'est pour la question 1 ??
arrivé a a(x²-Sx+P)
je dis que x1=... et x2.....
??
et pour la question 2 la phrase suffie?
barbot a écrit:mais ca c'est pour la question 1 ??
arrivé a a(x²-Sx+P)
je dis que x1=... et x2.....
??
et pour la question 2 la phrase suffie?
ha oki c'est a la fin ca pour demotrer que c'est bien egal a -b/a
et c/a
donc je suis d'accord pour la somme mais pour le produit je dois proceder a une multiplication
x1x2
mais je vois pas je dois mettre quoi
(-b+racine(delta)/2a ) fois (-b-racine(delta)/2a)
???
Re, soit que tu fais comme j'ai fait soit que tu fais ce qu'a fais Quidam dans l'autre post à savoir:
Quidam a écrit:exercice 1 :
soit P(x) un polynome du second degré qui admet 2 racines dinstinctes : x1 et x2
p(x) = ax²+bx+c
1) demontrer que la somme S des racines est egale à x1 +x2 = -b/a et que leur produit P est egal
à x1x2 = c/a
Puisque P(x1)=0 et que P(x2)=0, p(x) s'écrit : P(x)=a(x-x1)*(x-x2)
P(x)=a(x²-Sx+P)=ax²-aSx+aP
En identifiant les coeficients, on constate que : b=-aS et c=aP
d'où S=-b/a et P=c/a
2) demontrer alors que x1 et x2 sont solutions de l'equation : x² - S x + P = 0
x1 et x2 sont donc solution de l'équation P(x)=0 mais comme a est différent de zéro cette équation équivaut à l'équation : x²-Sx+P=0. Donc les solutions de x²-Sx+P sont x1 et x2
3) application ; trouver 2 nombres connaissant leur somme 18 et leur somme
72
Les deux nombres sont donc les solutions de l'équation : x²-18x+72
On résoud l'équation et on trouve 6 et 12.
--------------------------------------------------------------------------------
fonfon a écrit:Re, soit que tu fais comme j'ai fait soit que tu fais ce qu'a fais Quidam dans l'autre post à savoir:
a(x²-xx2-x1x+x1x2)
=a(xv-xx1-xx2+x1x2)
=a(x²-x(x1+x2)x1x2)
donc p(x)=a(x²-Sx+P)
comme x1 et x2 sont les racines du polinome p(x)=ax²+bx+c
alors p(x)=a(x-x1)(x-x2)
donc
x1=... x2=...
donc x1+x2=..-b/a
puis je fais avec x1x2
voila c'est bon?
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
