Salut a tous
Soit un=ln((1+1/n^2)(1+2/n^2)...(1+n/n^2)) je ne sais comment transformer cette equation il devrait avoir 1+2++3...+n et 1^2+2^2+...n^2 merci a tous :help:
Limite avec ln et suite
3 messages
- Page 1 sur 1
Considérons l'intervalle  =[1; 1+1/n] et les n réels 1+k/n², k=1à n, ils divisent l'intervalle
=[1; 1+1/n] et les n réels 1+k/n², k=1à n, ils divisent l'intervalle  en n parties égales et sur chaque intervalle [1+(k-1)/n²; 1+k/n²], on a ln(1+(k-1)/n²)
en n parties égales et sur chaque intervalle [1+(k-1)/n²; 1+k/n²], on a ln(1+(k-1)/n²))
 ln(1+k/n²); d'où
ln(1+k/n²); d'où
/n^2))
 dx)
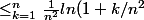) , soit
, soit
\leq)
(ln(1+1/n))-1/n)

 , soit encore
, soit encore \leq)
(ln(1+1/n)-n)

 .
.
Et voilà, je pensais qu'on pourrait s'en tirer dans le cadre du programme de terminale avec la méthode des rectangles, mais on est bloqué! Si on utilise le développement limité à l'ordre 2 de ln(x), soit
ln(x)=x-x²/2 +0(x²), où 0(x²) est un terme qui tend vers 0 infiniment plus vite que x², on trouve tout de suite que tend vers 1/2. Je ne vois pas comment faire autrement. Pour moi cet exercice est totalement hors programme. Mais, comme c'est à faire à la maison, on peut tricher un peu:
tend vers 1/2. Je ne vois pas comment faire autrement. Pour moi cet exercice est totalement hors programme. Mais, comme c'est à faire à la maison, on peut tricher un peu:
déjà, j'utilise le fait que F(x)=xln(x)-x est une primitive de f(x) =ln(x) sur ]0; +oo[; tu peut toujours dire que tu l'as vu dans un exercice et que tu as bien vérifié que F'(x)=ln(x);
ensuite on t'as parlé des d.l. (développements limités) et tu t'es renseigné et comme le d.l. de ln(1+x)
est un grand classique, tu as trouvé à l'ordre 2: =x-\frac{x^2}{2}+x^2\epsilon(x))
avec) qui tend vers 0 quand x tend vers 0, ce qui t'as donné :
qui tend vers 0 quand x tend vers 0, ce qui t'as donné :
 =\frac{1}{n}-\frac{1}{2n^2}+(\frac{1}{n^2})\epsilon(\frac{1}{n}))
avec) qui tend vers 0 quand n tend vers +oo.
qui tend vers 0 quand n tend vers +oo.
Poson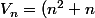(ln(1+1/n)-n) , il vient
, il vient 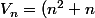(\frac{1}{n}-\frac{1}{2n^2}+\frac{1}{n^2}\epsilon(\frac{1}{n}))-n) =
= +1-\frac{1}{2n}+(\frac{1}{n})\epsilon(\frac{1}{n})+n)
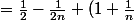\epsilon(\frac{1}{n})) donc
donc  converge vers
converge vers
 . Il reste à conclure pour
. Il reste à conclure pour  , ce que je te laisse faire..
, ce que je te laisse faire..
Et voilà, je pensais qu'on pourrait s'en tirer dans le cadre du programme de terminale avec la méthode des rectangles, mais on est bloqué! Si on utilise le développement limité à l'ordre 2 de ln(x), soit
ln(x)=x-x²/2 +0(x²), où 0(x²) est un terme qui tend vers 0 infiniment plus vite que x², on trouve tout de suite que
déjà, j'utilise le fait que F(x)=xln(x)-x est une primitive de f(x) =ln(x) sur ]0; +oo[; tu peut toujours dire que tu l'as vu dans un exercice et que tu as bien vérifié que F'(x)=ln(x);
ensuite on t'as parlé des d.l. (développements limités) et tu t'es renseigné et comme le d.l. de ln(1+x)
est un grand classique, tu as trouvé à l'ordre 2:
avec
avec
Poson
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
