Pouvez vous m'aider à démontrer cette inégalité?
a et b sont deux réesl supérieures à 1 et q un réel supérieure a 1.
Alors
(a+b)^q >= a^q + b^q.
Inegalite
6 messages
- Page 1 sur 1
Salut,
sauf erreur, c'est même vrai pour tout a,b>=0.
Il y a des tas de façons de le démontrer.
L'une des plus élémentaire est d'étudier la fonction=(x+b)^q-x^q) sur
sur 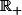 (avec
(avec 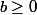 fixé).
fixé).
Elle est dérivable et=q\Big((x+b)^{q-1}-x^{q-1}\big)\geq0) car, vu que
car, vu que 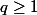 , la fonction
, la fonction  est croissante.
est croissante.
Donc est croissante et, en particulier, pour tout
est croissante et, en particulier, pour tout 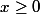 ,
, \geq f(0)=b^q)
EDIT : grilled par zygomatique...
sauf erreur, c'est même vrai pour tout a,b>=0.
Il y a des tas de façons de le démontrer.
L'une des plus élémentaire est d'étudier la fonction
Elle est dérivable et
Donc
EDIT : grilled par zygomatique...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
