Aide Trigonométrie factorisation
14 messages
- Page 1 sur 1
Aide Trigonométrie factorisation
Bonjour a tous, je suis en 1ère S
Donc voila je doit trouver les solutions de: 1/2 X cosx - ("racine"3)/2 X sinx =1
sur R.
On sait qu'on peut identifier cette expression a une expression de la forme sin(x-a),
je pensais a sa moi: -sin(a-x)= sin(;)/6) X cos(x) - cos (;)/6) X sin(x)
Si vous pouviez m'aider sa serait super :)
merci d'avance
Donc voila je doit trouver les solutions de: 1/2 X cosx - ("racine"3)/2 X sinx =1
sur R.
On sait qu'on peut identifier cette expression a une expression de la forme sin(x-a),
je pensais a sa moi: -sin(a-x)= sin(;)/6) X cos(x) - cos (;)/6) X sin(x)
Si vous pouviez m'aider sa serait super :)
merci d'avance
Pas besoin de changer sin(x-a) en -sin(a-x) même si c'est vrai.
L'important est de "rétrécir" l'expression en un seul sinus pour appliquer la méthode de résolution.
On utilise la formule : = \sin a \cos b - \cos a \sin b) qui se lit aussi bien en sens inverse comme toute égalité, c'est à dire que
qui se lit aussi bien en sens inverse comme toute égalité, c'est à dire que 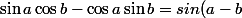) est vraie aussi.
est vraie aussi.
Ton idée est donc bonne mais l'écriture est fausse.
Réécris la formule en remplaçant rigoureusement dans la formule du cours les paramètres a et b par ce qui convient d'après l'énoncé.
L'important est de "rétrécir" l'expression en un seul sinus pour appliquer la méthode de résolution.
On utilise la formule :
Ton idée est donc bonne mais l'écriture est fausse.
Réécris la formule en remplaçant rigoureusement dans la formule du cours les paramètres a et b par ce qui convient d'après l'énoncé.
on me demande par la suite d'utiliser le même principe de factorisation que précédemment pour compléter:
1) cosx + sinx = ... sin(x+...)
2) cosx + sinx = ...cos(x+...)
3) cosx + ;)3sinx = ...sin(x+...)
4) cosx + ;)3sinx = ... cos(x+...)
5);)3cosx - sinx = ... sin(x+...)
Sauf que je ne vois pas trop par ou attaquer.
J'ai bien pensée au carré avec la formule cos²x+sin²x=1 mais sa ne me mène pas a grand chose.
Es-que vous auriez une idée de la marche a suivre, ou de comment procéder ?
Toute aide sera la bien venus :we: merci d'avance
1) cosx + sinx = ... sin(x+...)
2) cosx + sinx = ...cos(x+...)
3) cosx + ;)3sinx = ...sin(x+...)
4) cosx + ;)3sinx = ... cos(x+...)
5);)3cosx - sinx = ... sin(x+...)
Sauf que je ne vois pas trop par ou attaquer.
J'ai bien pensée au carré avec la formule cos²x+sin²x=1 mais sa ne me mène pas a grand chose.
Es-que vous auriez une idée de la marche a suivre, ou de comment procéder ?
Toute aide sera la bien venus :we: merci d'avance
Salut !
1) Tu sais que=\sin(a)\cos(b)+\cos(a)\sin(b)) donc cherche
donc cherche  tel que
tel que =\cos(a)) :+++:
:+++:
2) Même idée avec) :++:
:++:
En multipliant de part et d'autre par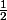 , il te suffit de te rappeler que
, il te suffit de te rappeler que  et
et  :+++:
:+++:
lancovi a écrit:1) cosx + sinx = ... sin(x+...)
2) cosx + sinx = ...cos(x+...)
1) Tu sais que
2) Même idée avec
lancovi a écrit:3) cosx +3sinx = ...sin(x+...)
4) cosx +3sinx = ... cos(x+...)
5);)3cosx - sinx = ... sin(x+...)
En multipliant de part et d'autre par
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
lancovi a écrit:Bien sur !!! enfaite cosx+sinx peut aussi être 1*cosx+1*sinx
avec sin... =1 et cos...=1
Merci ! je reprend confiance en moi
Il n'existe pas d'angle dont le cos et le sin soient égaux à 1. Mais tu es sur la bonne voie : faire apparaître des valeurs invisibles !
Par contre il existe un angle dont le cos et le sin sont identiques. Lequel est-ce ?
Si tu regardes bien la solution, il y a un coefficient à trouver au sinus du résultat, ce qui indique une factorisation.
Cette astuce est difficile à trouver quand on ne la connait pas mais elle reviendra régulièrement en maths.
lancovi a écrit:a bon ? A moins que je ne me sois mal exprimépourtant cos(0)=1 je crois ?
et sin(pi/2)=1 également ?
C'est juste mais les angles sont différents.
Donc grâce a vous :)
J'arrive après factorisation de ;)2/2 a
cosx+sinx= -;)2/2*sin( x+ pi/4 )
La question que je me pose maintenant est: es-quil m'est aussi demandé de déterminé x ou non ? je n'ai pas d'autres information dans l'énoncé que " En utilisant le principe de factorisation de l'exercice précédent, recopier et compléter les transformation "
Vous en pensez quoi ?
J'arrive après factorisation de ;)2/2 a
cosx+sinx= -;)2/2*sin( x+ pi/4 )
La question que je me pose maintenant est: es-quil m'est aussi demandé de déterminé x ou non ? je n'ai pas d'autres information dans l'énoncé que " En utilisant le principe de factorisation de l'exercice précédent, recopier et compléter les transformation "
Vous en pensez quoi ?
lancovi a écrit:Donc grâce a vous
J'arrive après factorisation de2/2 a
cosx+sinx= -;)2/2*sin( x+ pi/4 )
La question que je me pose maintenant est: es-quil m'est aussi demandé de déterminé x ou non ? je n'ai pas d'autres information dans l'énoncé que " En utilisant le principe de factorisation de l'exercice précédent, recopier et compléter les transformation "
Vous en pensez quoi ?
apparemment non : on te demande juste de compléter des "trous" pour obtenir des égalités vraies quel que soit le réel
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Ce n'est pas tout à fait ça.
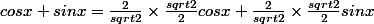
soit après factorisation par la valeur qui nous "dérange" :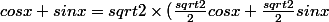=sqrt2 sin (\frac{\pi}{4} + x))
Je te conseille de vérifier à la calculatrice avec quelques valeurs numériques, en n'oubliant pas de la mettre en mode radian. Ce réflexe de vérification te permettra d'éviter quelques erreurs.
soit après factorisation par la valeur qui nous "dérange" :
Je te conseille de vérifier à la calculatrice avec quelques valeurs numériques, en n'oubliant pas de la mettre en mode radian. Ce réflexe de vérification te permettra d'éviter quelques erreurs.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
