Ressort - energie
18 messages
- Page 1 sur 1
ressort - energie
Bonjour à tous , j'ai l'exercice suivant que j'ai réalisé , j'aimerais savoir si j'ai bon svp :
Un ressort idéal à réponse linéaire a pour longueur à vide l = 25cm. Sous l'action d'une force de 5N , il s'allonge de 10cm.
1) Calculer la constante de raideur du ressort .
Sa constante raideur est de k = 5*10 = 50N/m .
2) ON fixe l'extrémité supérieure du ressort et on accroche à l'extrémité inférieure un corps A de masse m = 200g . Calculer l'allongement a du ressort quand A est en équilibre . (1)
Le corps A exerce une force de 10*0.2 = 2 N sur le ressort , l'allongement du ressort est donc de 100/25 , soit 4cm .
3) On écarte A de la position d'équilibre verticalement vers le bas d'une distance d = 3cm . (2)
a) donner les caractéristiques de la force qu'il faut exercer sur A pour le maintenir dans sa nouvelle position .
La force doit être de direction verticale , vers le bas et de valeur F = 350/100 = 3.5N .
b) entre les positions (1) et (2) calculer :
-la variation d'énergie potentielle élastique .
Epf - Epi = 1/2 * 50 * -0.07² - 1/2 * 50 * -0.04² = -0.0825 J
-la variation d'énergie potentielle de pesanteur.
Je choisis comme point de référence le bout du ressort par lequel est accrochée la masse A .
m.g(zf - zi) = 0.2*10(-0.07-(-0.04)) = -0.06J
-la variation d'énergie mécanique de l'ensemble ressort + corps A placé dans le champ de pesanteur .
(Epf + m.g.zf) - (Epi + m.g.zi) = ( -0.1225 - 0.014 ) - ( -0.04 - 0.008 ) = -0.1045 J
Ici j'ai considéré que l'énergie mécanique du système c'était énergie potentielle de pesanteur + énergie potentielle élastique , je savais pas quoi faire vu que en réalité l'énergie mécanique c'est énergie potentille + énergie cinétique .
- le travail fournit pour amener A d'une position à l'autre
W(P) = -Ep ( variation ) = 0.1045J .
merci
Un ressort idéal à réponse linéaire a pour longueur à vide l = 25cm. Sous l'action d'une force de 5N , il s'allonge de 10cm.
1) Calculer la constante de raideur du ressort .
Sa constante raideur est de k = 5*10 = 50N/m .
2) ON fixe l'extrémité supérieure du ressort et on accroche à l'extrémité inférieure un corps A de masse m = 200g . Calculer l'allongement a du ressort quand A est en équilibre . (1)
Le corps A exerce une force de 10*0.2 = 2 N sur le ressort , l'allongement du ressort est donc de 100/25 , soit 4cm .
3) On écarte A de la position d'équilibre verticalement vers le bas d'une distance d = 3cm . (2)
a) donner les caractéristiques de la force qu'il faut exercer sur A pour le maintenir dans sa nouvelle position .
La force doit être de direction verticale , vers le bas et de valeur F = 350/100 = 3.5N .
b) entre les positions (1) et (2) calculer :
-la variation d'énergie potentielle élastique .
Epf - Epi = 1/2 * 50 * -0.07² - 1/2 * 50 * -0.04² = -0.0825 J
-la variation d'énergie potentielle de pesanteur.
Je choisis comme point de référence le bout du ressort par lequel est accrochée la masse A .
m.g(zf - zi) = 0.2*10(-0.07-(-0.04)) = -0.06J
-la variation d'énergie mécanique de l'ensemble ressort + corps A placé dans le champ de pesanteur .
(Epf + m.g.zf) - (Epi + m.g.zi) = ( -0.1225 - 0.014 ) - ( -0.04 - 0.008 ) = -0.1045 J
Ici j'ai considéré que l'énergie mécanique du système c'était énergie potentielle de pesanteur + énergie potentielle élastique , je savais pas quoi faire vu que en réalité l'énergie mécanique c'est énergie potentille + énergie cinétique .
- le travail fournit pour amener A d'une position à l'autre
W(P) = -Ep ( variation ) = 0.1045J .
merci
Bonsoir,
voici des explications
F = k(l-l0) ; j'appelle a = l-l0 (avec l0: lg à vide et l: lg en tension)
soit F=ka et k=F/a
donc k = 5/ (10*10^(-2)) (je mets 1O cm en unité S.I. soit en m)
(ça revient à 5*10 mais les calculs viennent de là)
En fait tu avais peut-être déjà fait cela!
Dans ce cas mea culpa!
Pour la 2ème:
à l'équilibre F=P donc k*a=m*g
a=m*g/k
a=0,2*10/50
a= 0.04m soit 4 cm
Attention, bien sûr, je n'écris pas tout
La relation F=P vient de la relation vectorielle F+P=0)
Bonne continuation
voici des explications
F = k(l-l0) ; j'appelle a = l-l0 (avec l0: lg à vide et l: lg en tension)
soit F=ka et k=F/a
donc k = 5/ (10*10^(-2)) (je mets 1O cm en unité S.I. soit en m)
(ça revient à 5*10 mais les calculs viennent de là)
En fait tu avais peut-être déjà fait cela!
Dans ce cas mea culpa!
Pour la 2ème:
à l'équilibre F=P donc k*a=m*g
a=m*g/k
a=0,2*10/50
a= 0.04m soit 4 cm
Attention, bien sûr, je n'écris pas tout
La relation F=P vient de la relation vectorielle F+P=0)
Bonne continuation
Salut neva,
1)



2)
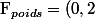(9,8) = 1,96 N$)


3)
a)
Ici je ne suis pas d'accord avec toi. Deux facons différentes me mène au même résultat mais différent du tien. Si j'oubli la position d'équilibre, et que j'amene directement le bloc a (0,03+0,0392)m de distance du ressort au repos, il y a 3 forces dans le systèmes. Il y a le poids, qui tire vers le bas, il y a la force du ressort qui tire vers le haut, et il y a la force nécessaire pour maintenir le ressort a 0,0692m de la position de repos du ressort également vers le bas. On se retrouver donc avec:

(0,0692) - (0,2)(9,8) = 1,5N$)
D'une facon équivalente, si on considere le bloc au départ a sa position d'équilibre, on peut assumer que le poids et la force du ressort s'annule. Donc il ne reste que la force que nous cherchons qui agit, donc:
(0,03) = 1,5N$)
Vérifie si j'ai raison pour etre sure.
b)
} - E_{elastique(i)} = (0,5)(50)(0,0692^2) - (0,5)(50)(0,0392)^2 = 0,0813 J$)
Je ne croix pas que ta réponse négative soit bonne, car premièrement ca ne marche pas mathématiquement, et intuitivement non plus. Une variation négative veux dire qu'a la fin il y a moins d'énergie potentielle qu'au début, mais pense-y, plus on étire un ressort, plus il veut revenir a sa position d'équilibre, donc plus il a d'énergie potentielle.
} - E_{pesanteur(i)} = (0,2)(9,8)(-0,03) - (0,2)(9,8)(0) = -0,0588J$)
Le négatif est logique, puisque moins il est haut, moins il a d'énergie potentielle due a la pesanteur, donc a la fin il en a moins qu'au début.
L'énergie mécanique est:
 par définition, pour un système bloc-ressort. (les variations des énergies potentielles j'entends ici).
par définition, pour un système bloc-ressort. (les variations des énergies potentielles j'entends ici).
Donc,

Pour ta question, je vais tenter d'y répondre. Au départ, le but est de trouver une équation qui nous permet de décrire le comportement d'un ressort par rapport a la force qu'on lui fait subir. Dans la question, on te dis déja que la relation est linéaire, donc qu'elle est de forme:

La il faut se demander qui est la variable indépendant dans le problème, est-ce la force qu'on applique qui dépend de la distance a laquelle le ressort s'étire, ou est-ce que la distance a laquelle le ressort s'étire dépend de la force qu'on lui applique? Il est évident que c'est la deuxième hypothèse qui est bonne. Donc, F est la variable indépendante, et x est la variable dépendante. On a alors:

Ensuite, il faut s'occuper du 'b'. Si la force qu'on applique est 0, de combien le ressort sera-t-il étiré? Il sera nullement étiré bien sur, tu peux le remarquer dans la vie de tout les jours avec un ressort, donc, on a:
 + b= b$)
Maintenant que nous savons que b=0, nous pouvons écrire l'équation comme cela:
 , ou on a simplement renommer 'a' par 'k', donc:
, ou on a simplement renommer 'a' par 'k', donc:

Ou F est la force du ressort et x son étirement. J'espère avoir répondu a tes questions.
1)
2)
3)
a)
Ici je ne suis pas d'accord avec toi. Deux facons différentes me mène au même résultat mais différent du tien. Si j'oubli la position d'équilibre, et que j'amene directement le bloc a (0,03+0,0392)m de distance du ressort au repos, il y a 3 forces dans le systèmes. Il y a le poids, qui tire vers le bas, il y a la force du ressort qui tire vers le haut, et il y a la force nécessaire pour maintenir le ressort a 0,0692m de la position de repos du ressort également vers le bas. On se retrouver donc avec:
D'une facon équivalente, si on considere le bloc au départ a sa position d'équilibre, on peut assumer que le poids et la force du ressort s'annule. Donc il ne reste que la force que nous cherchons qui agit, donc:
Vérifie si j'ai raison pour etre sure.
b)
Je ne croix pas que ta réponse négative soit bonne, car premièrement ca ne marche pas mathématiquement, et intuitivement non plus. Une variation négative veux dire qu'a la fin il y a moins d'énergie potentielle qu'au début, mais pense-y, plus on étire un ressort, plus il veut revenir a sa position d'équilibre, donc plus il a d'énergie potentielle.
Le négatif est logique, puisque moins il est haut, moins il a d'énergie potentielle due a la pesanteur, donc a la fin il en a moins qu'au début.
L'énergie mécanique est:
Donc,
Pour ta question, je vais tenter d'y répondre. Au départ, le but est de trouver une équation qui nous permet de décrire le comportement d'un ressort par rapport a la force qu'on lui fait subir. Dans la question, on te dis déja que la relation est linéaire, donc qu'elle est de forme:
La il faut se demander qui est la variable indépendant dans le problème, est-ce la force qu'on applique qui dépend de la distance a laquelle le ressort s'étire, ou est-ce que la distance a laquelle le ressort s'étire dépend de la force qu'on lui applique? Il est évident que c'est la deuxième hypothèse qui est bonne. Donc, F est la variable indépendante, et x est la variable dépendante. On a alors:
Ensuite, il faut s'occuper du 'b'. Si la force qu'on applique est 0, de combien le ressort sera-t-il étiré? Il sera nullement étiré bien sur, tu peux le remarquer dans la vie de tout les jours avec un ressort, donc, on a:
Maintenant que nous savons que b=0, nous pouvons écrire l'équation comme cela:
Ou F est la force du ressort et x son étirement. J'espère avoir répondu a tes questions.
je ne suis absolument pas d'accord pour tes calculs sur la question 3) , j'ai appliqué rigouresement les formules , je suis certain des 3.45N pour le a) , pour le b) je suis certain d'avoir bon jusqu'aux énergies potentielles , c'est lénergie mécanique dont je ne suis pas sur du tout .
Je répète , j'ai bien appliqué les formules .
Je répète , j'ai bien appliqué les formules .
Resalut,
peut-etre est tu un peu borné lol?
Tu as dis:
Epf - Epi = 1/2 * 50 * -0.07² - 1/2 * 50 * -0.04² = -0.0825 J
Je fais le calcul:
25 * (-0,07)² - 25 (-0,04)² = 0,1225 - 0,04 = 0,0825 J, ta reponse n'est pas bonne, tu as un moins.
Pour le reste on a les memes réponses dans les énergies. J'comprend meme pas pourquoi tu dis que tu n'es pas daccord? la seule réponse qui diffère c'est la force. Je trouve ca un peu arrogant ton attitude. On est la pour aider, si t'es pas près a recevoir de l'aide ou a discuter de ton problème ne post meme pas. Maintenant, si tu peux y aller un peu plus poliement, surtout que j'ai pris de mon temps pour repondre a tes questions, explique moi comment tu as trouvé la force.
P.S. Je pense que tu as fais:

Or, c'est faux, le poids n'est pas dans le même sens que la force du ressort.
peut-etre est tu un peu borné lol?
Tu as dis:
Epf - Epi = 1/2 * 50 * -0.07² - 1/2 * 50 * -0.04² = -0.0825 J
Je fais le calcul:
25 * (-0,07)² - 25 (-0,04)² = 0,1225 - 0,04 = 0,0825 J, ta reponse n'est pas bonne, tu as un moins.
Pour le reste on a les memes réponses dans les énergies. J'comprend meme pas pourquoi tu dis que tu n'es pas daccord? la seule réponse qui diffère c'est la force. Je trouve ca un peu arrogant ton attitude. On est la pour aider, si t'es pas près a recevoir de l'aide ou a discuter de ton problème ne post meme pas. Maintenant, si tu peux y aller un peu plus poliement, surtout que j'ai pris de mon temps pour repondre a tes questions, explique moi comment tu as trouvé la force.
P.S. Je pense que tu as fais:
Or, c'est faux, le poids n'est pas dans le même sens que la force du ressort.
bien sur , voici le détail de mon calcul pour la force :
La force doit être de direction verticale , vers le bas . L'allongement total est donc de 6.9cm , donc la force totale pour maintenir le ressort dans cette position est F = 50 * 0.069 = 3.45N .
Pour l'énergie mécanique on ne trouve pas le même résultat .
La force doit être de direction verticale , vers le bas . L'allongement total est donc de 6.9cm , donc la force totale pour maintenir le ressort dans cette position est F = 50 * 0.069 = 3.45N .
Pour l'énergie mécanique on ne trouve pas le même résultat .
Tu ne peux pas faire F = 50 * 0,069... parce qu'en faisant ca, tu dis qu'il faut exercer une force depuis la position de repos du ressort jusqua la position finale du bloc. Sauf que c'est pas ca la question. La question c'est: en partant du point d'équilibre du ressort avec le bloc (donc 4cm), on tire le boc 3cm vers le bas et on veut connaitre la force quil faut exercer pour le maintenir la. Tas pas besoin de force pour amener le bloc jusqua 4cm, le poids s'en charche déja. La seule force que tu dois appliquer c'est entre 4cm et 7 cm. Ton résultat n'est pas correct.
Pour l'énergie mécanique c'est normal qu'on ai pas la meme réponse, tu fais:
(Epf + m.g.zf) - (Epi + m.g.zi) = ( -0.1225 - 0.014 ) - ( -0.04 - 0.008 ) = -0.1045 J
Sauf que, Epf = 0,5 * 50 * (-0,07)^2 = 0,1225 , et NON -0,1225.
et que m.g.zf = 0,2 * 10 * -0,07 = -0,14, et NON -0,014
et que m.g.zi = 0,2 * 10 * -0,04 = -0,08 et NON -0,008
et que Epi = 0,5 * 50 * (-0,040)^2 = 0,04 et NON -0,04, car on te demande pas une variation, yas pas de moins la.
Donc finalement, en corrigeant tes erreurs, ca devient:
(Epf + m.g.zf) - (Epi + m.g.zi) = ( 0.1225 - 0.14 ) - ( 0.04 - 0.08 ) = 0,0225 J
Pour l'énergie mécanique c'est normal qu'on ai pas la meme réponse, tu fais:
(Epf + m.g.zf) - (Epi + m.g.zi) = ( -0.1225 - 0.014 ) - ( -0.04 - 0.008 ) = -0.1045 J
Sauf que, Epf = 0,5 * 50 * (-0,07)^2 = 0,1225 , et NON -0,1225.
et que m.g.zf = 0,2 * 10 * -0,07 = -0,14, et NON -0,014
et que m.g.zi = 0,2 * 10 * -0,04 = -0,08 et NON -0,008
et que Epi = 0,5 * 50 * (-0,040)^2 = 0,04 et NON -0,04, car on te demande pas une variation, yas pas de moins la.
Donc finalement, en corrigeant tes erreurs, ca devient:
(Epf + m.g.zf) - (Epi + m.g.zi) = ( 0.1225 - 0.14 ) - ( 0.04 - 0.08 ) = 0,0225 J
Salut,
pour la relation:

j'en ai jamais entendu parlé donc je ne sais pas si elle est vraie... mais dans ce cas précis ce n'est pas ce que l'on cherche, car on veut amener A de la position d'équilibre(4cm) a 7cm. La force en jeu est donc:

et le travail est:

C'est une intégrale parce que la force n'est pas constante sur le trajet, elle change. Ce n'est pas comme si je poussais une auto du point A au point B avec une force constante. Vue que la force change sans cesse, tu dois découper le trajet en morceaux infiniment petit pour que la force soit juger constante.
/2$)
Donc,
^2 = 0,0225J$)
En fait, dans ce cas-ci, le travail est égal a l'énergie mécanique, car c'est l'énergie mécanique.
pour la relation:
j'en ai jamais entendu parlé donc je ne sais pas si elle est vraie... mais dans ce cas précis ce n'est pas ce que l'on cherche, car on veut amener A de la position d'équilibre(4cm) a 7cm. La force en jeu est donc:
et le travail est:
C'est une intégrale parce que la force n'est pas constante sur le trajet, elle change. Ce n'est pas comme si je poussais une auto du point A au point B avec une force constante. Vue que la force change sans cesse, tu dois découper le trajet en morceaux infiniment petit pour que la force soit juger constante.
Donc,
En fait, dans ce cas-ci, le travail est égal a l'énergie mécanique, car c'est l'énergie mécanique.
En fait, ta formule est correcte, et ca reviens au meme que la mienne. Ton erreur et que tu as pris 7cm et 4cm...ce n'est pas vrai! la force commence a s'appliquer a 4cm et finit de s'appliquer a 7cm, d'accord, mais cela veut dire qu'elle n'a été appliqué que de sa position d'équilibre (0cm hypothétique) a sa position finale (3 cm hypothétique). En mettant 4 cm, tu calcul aussi le travail fait avant sa position d'équilibre, tu comprends? Pour rectifier ton calcul serait:
25 * (0.03*0.03 - 0*0) = 0.0225J
25 * (0.03*0.03 - 0*0) = 0.0225J
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
