Meca
16 messages
- Page 1 sur 1
meca
bonjour tout le monde,
voici le prob
Quelle est en Newton le module de la force necessaire pour arreter en 50 mètre un véhicule de 800kg se dépacant à 72km/h sur une route horizontale?
J'ai cherché mais je vois pas du tt comment je peux faire pour résoudre ce prob.
J'imagine selon l'énoncé qu'on doit négliger les forces de frottement...
Merci de votre aide
voici le prob
Quelle est en Newton le module de la force necessaire pour arreter en 50 mètre un véhicule de 800kg se dépacant à 72km/h sur une route horizontale?
J'ai cherché mais je vois pas du tt comment je peux faire pour résoudre ce prob.
J'imagine selon l'énoncé qu'on doit négliger les forces de frottement...
Merci de votre aide
est ce que dans ce cas le poids et la réaction au sol se compensent?
parce que dans ce cas là on a :
F = m*a (F et a des vecteurs ou a et l'acceleration..et F la foce lié à la vitesse..je sais pas comment on l'appelle)
F = m*dv/dt
miantenant je ne sais pas comment on fait pour calculé dv/dt...il faut qu'en 50mètres le véhicule lancé à 72km/h soit arretée..
parce que dans ce cas là on a :
F = m*a (F et a des vecteurs ou a et l'acceleration..et F la foce lié à la vitesse..je sais pas comment on l'appelle)
F = m*dv/dt
miantenant je ne sais pas comment on fait pour calculé dv/dt...il faut qu'en 50mètres le véhicule lancé à 72km/h soit arretée..
bon finalement (triple post..dsl..)
g trouvé une formule..qui est sorti comme ca..d=a*t²/2+V*t ou V est la vitesse initiale et d la distance à parcourir
on a aussi la relation Vf=a*t + V ou Vf est la vitesse final..cad 0
en mélangeant le tout on trouve la que dv/dt =-4m/s
d'ou le module de la force est de 3200N
maintenant ma question est...d'ou sort cette formule..elle vient d'ou et comment on l'a démontre??
d=a*t²/2+V*t
Merci
g trouvé une formule..qui est sorti comme ca..d=a*t²/2+V*t ou V est la vitesse initiale et d la distance à parcourir
on a aussi la relation Vf=a*t + V ou Vf est la vitesse final..cad 0
en mélangeant le tout on trouve la que dv/dt =-4m/s
d'ou le module de la force est de 3200N
maintenant ma question est...d'ou sort cette formule..elle vient d'ou et comment on l'a démontre??
d=a*t²/2+V*t
Merci
Salut,
il suffit de prendre un vecteur directeur de la droite représentant la route, et de noter par
directeur de la droite représentant la route, et de noter par  la position du véhicule,
la position du véhicule,  représentant donc son abscisse et étant une fonciton du temps.
représentant donc son abscisse et étant une fonciton du temps.
Ensuite, tu appliques tout simplement la RFD (Relation Fondamentale de la Dynamique) :
 (force appliquée pour que le véhicule s'arrête)
(force appliquée pour que le véhicule s'arrête)
donc
donc + k\vec{i} = -Ft\vec{i} + k\vec{i})
( étant une constante due à la primitivation)
étant une constante due à la primitivation)
soit donc = -Ft\vec{i} + k \vec{i}) ,
,
ensuite, tu utilises le fait que) est donnée dans l'énoncé et tu traduis cela dans l'équation ci-dessus, tu trouves ainsi la constante
est donnée dans l'énoncé et tu traduis cela dans l'équation ci-dessus, tu trouves ainsi la constante  , reste alors à traduire, toujours dans l'équation ci-dessus, que l'on connait le temps
, reste alors à traduire, toujours dans l'équation ci-dessus, que l'on connait le temps 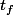 au bout duquel elle va s'arrêter (et donc
au bout duquel elle va s'arrêter (et donc  = 0) ),
),
et le problème est résolu.
:happy3:
il suffit de prendre un vecteur
Ensuite, tu appliques tout simplement la RFD (Relation Fondamentale de la Dynamique) :
donc
donc
(
soit donc
ensuite, tu utilises le fait que
et le problème est résolu.
:happy3:
....Et je dirais même plus.......
A défaut de te lancer dans des primitivations pas toujours évidentes, tu peux toujours employer le théorème de l'énergie cinétique.

différence d'énergie cinétique sur le trajet d= somme des travaux des forces en action sur le trajet d.
donc en sachant que
0-mv²/2=-d*F F la force d'arrêt, d la distance d'arrêt
alors F= .
.
Sinon, pour ce qui de ta formule, il s'agit de l'équation horaire du déplacement d'un objet de vitesse initiale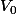 =72km/h
=72km/h
le mouvement est ralenti donc a=-k k réel positif.
a=dv/dt, dont par primitivation on a V=-kt+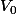
V=dx/dt de même X= or Xo=0
or Xo=0
C'est donc de là que vient ta formule,
sinon le , est un vecteur unitaire qui sert simplement à orienter l'axe de déplacement pour différencier les mouvements dans un sens précis k
, est un vecteur unitaire qui sert simplement à orienter l'axe de déplacement pour différencier les mouvements dans un sens précis k ou dans le sens contraire -k
ou dans le sens contraire -k .
.
ainsi,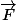 veut stopper la voiture en s'opposant au déplacement de la voiture qui est selon
veut stopper la voiture en s'opposant au déplacement de la voiture qui est selon 
J'espère que tout est plus clair maintenant.
différence d'énergie cinétique sur le trajet d= somme des travaux des forces en action sur le trajet d.
donc en sachant que
0-mv²/2=-d*F F la force d'arrêt, d la distance d'arrêt
alors F=
Sinon, pour ce qui de ta formule, il s'agit de l'équation horaire du déplacement d'un objet de vitesse initiale
le mouvement est ralenti donc a=-k k réel positif.
a=dv/dt, dont par primitivation on a V=-kt+
V=dx/dt de même X=
C'est donc de là que vient ta formule,
sinon le
ainsi,
J'espère que tout est plus clair maintenant.
Tu as l'équation  = -Ft\vec{i} + k \vec{i}) ,
,
Or) est selon
est selon  , donc l'équation devient
, donc l'équation devient
mV(t) = -Ft + k (cela revient à faire le produit scalaire de tout par le vecteur i, et donc tu te débarasses du i)
Comme tu connais V(t=0), tu as donc, en prenant t=0 dans l'équation ci-dessus,
mV(0) = k
Ensuite tu connais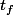 (donné dans l'énoncé) et à
(donné dans l'énoncé) et à 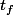 ,
,
la vitesse vaut 0,
donv 0 = -F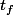 + k,
+ k,
donc F = k/(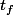 ) = mV(0)/(
) = mV(0)/(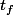 )
)
:happy3:
Or
mV(t) = -Ft + k (cela revient à faire le produit scalaire de tout par le vecteur i, et donc tu te débarasses du i)
Comme tu connais V(t=0), tu as donc, en prenant t=0 dans l'équation ci-dessus,
mV(0) = k
Ensuite tu connais
la vitesse vaut 0,
donv 0 = -F
donc F = k/(
:happy3:
Oui, tu as raison, j'avais mal lu l'énoncé.
Grâce à l'équation = -Ft\vec{i} + k \vec{i}) ,
,
tu obtiens k = mV(0) (la vitesse est V(0) à t=0)
tu obtiens aussi l'expression de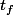 en fonction de F :
en fonction de F :
}{F}) .
.
Ensuite, tu primitives chaque membre de l'équation = -Ft\vec{i} + mV(0) \vec{i}) ,
,
et tu obtiens donc (après un produit scalaire par i)
 = -(1/2)Ft^{2} + mV(0)t + k')
et tu dois donc déterminer une constante k', tu la détermines en fixant x(0) = 0.
Ensuite, tu connais k et k', et tu connais ,
,
de plus tu connais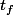 en fonction de F,
en fonction de F,
et donc de l'équation
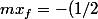Ft_f^{2} + mV(0)t_f + k') , tu trouves la valeur de F.
, tu trouves la valeur de F.
Je reconnais que ce n'est pas forcément la façon la plus simple de procéder, mais j'avais mal lu le début de l'énonce : je croyais avoir lu 50 secondes, alors que c'était 50 mètres... Autant pour moi.
Cependant, quand on a l'habitude, on arrive très vite au résultat (les équations se résolvent de manière "instantanée").
:happy3:
Grâce à l'équation
tu obtiens k = mV(0) (la vitesse est V(0) à t=0)
tu obtiens aussi l'expression de
Ensuite, tu primitives chaque membre de l'équation
et tu obtiens donc (après un produit scalaire par i)
et tu dois donc déterminer une constante k', tu la détermines en fixant x(0) = 0.
Ensuite, tu connais k et k', et tu connais
de plus tu connais
et donc de l'équation
Je reconnais que ce n'est pas forcément la façon la plus simple de procéder, mais j'avais mal lu le début de l'énonce : je croyais avoir lu 50 secondes, alors que c'était 50 mètres... Autant pour moi.
Cependant, quand on a l'habitude, on arrive très vite au résultat (les équations se résolvent de manière "instantanée").
:happy3:
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
